5 Ways to Solve Systems of Inequalities Graphically
Understanding Systems of Inequalities
Systems of inequalities are a crucial concept in mathematics, particularly in algebra and calculus. They involve solving a set of inequalities that contain two or more variables. These systems can be solved using various methods, including graphical, algebraic, and numerical approaches. In this blog post, we will focus on solving systems of inequalities graphically.
What are Systems of Inequalities?
A system of inequalities is a set of two or more inequalities that contain the same variables. These inequalities can be linear or nonlinear, and they can be equalities (equations) or inequalities (strict or non-strict). For example:
2x + 3y > 5 x - 2y ≤ 3
This system consists of two linear inequalities in two variables, x and y.
Why Solve Systems of Inequalities Graphically?
Graphical methods are a powerful way to visualize and solve systems of inequalities. By graphing the inequalities on a coordinate plane, we can identify the regions that satisfy all the inequalities in the system. This approach is particularly useful when dealing with systems of linear inequalities.
5 Ways to Solve Systems of Inequalities Graphically
1. Graphing Individual Inequalities
To solve a system of inequalities graphically, start by graphing each inequality separately on a coordinate plane. Use a solid line for non-strict inequalities (≤, ≥) and a dashed line for strict inequalities (<, >). Shade the region that satisfies each inequality.
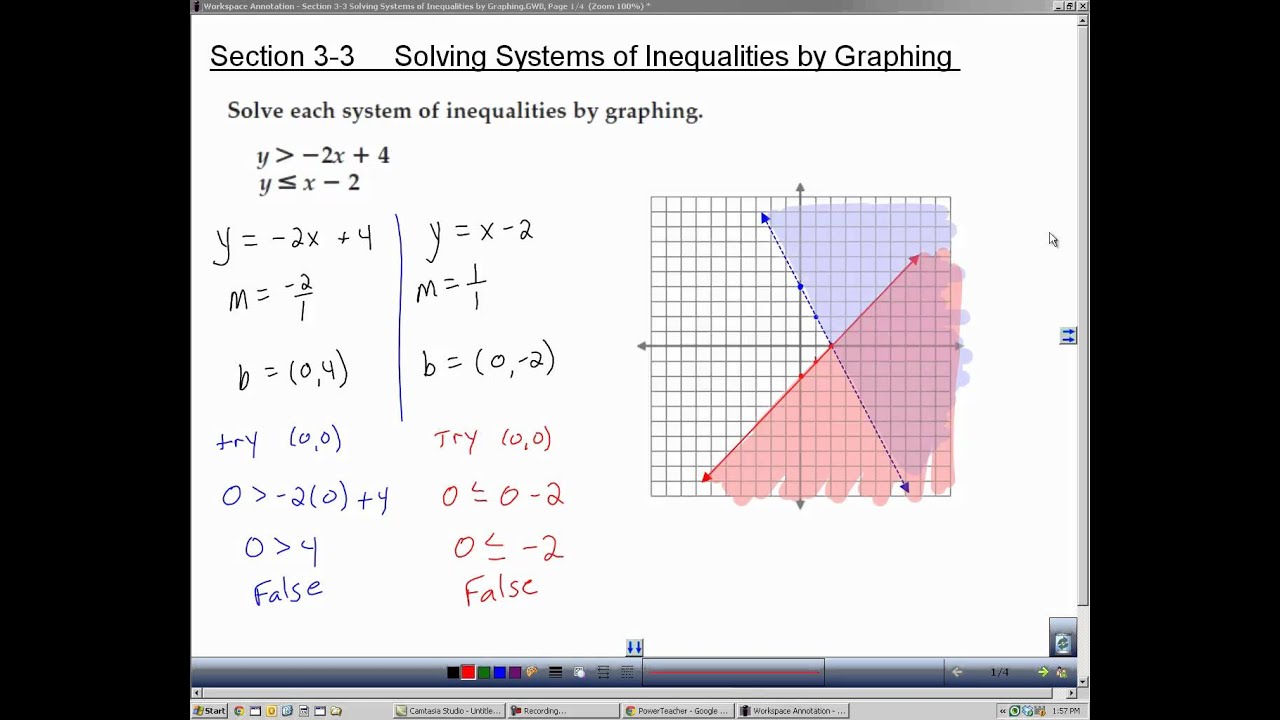
| Inequality | Graph |
|---|---|
| 2x + 3y > 5 | Dashed line with shading above the line |
| x - 2y ≤ 3 | Solid line with shading below the line |
2. Identifying the Solution Region
Once you have graphed all the inequalities, identify the region that satisfies all the inequalities in the system. This region is the solution to the system of inequalities.
📝 Note: The solution region may be a single point, a line segment, or a region bounded by lines.
3. Using Test Points
To determine which side of a line satisfies an inequality, use a test point. Choose a point that is clearly on one side of the line and substitute the coordinates into the inequality. If the inequality is true, then the point is in the solution region.
4. Graphing Systems with Three or More Inequalities
When dealing with systems of three or more inequalities, graph each inequality separately and identify the regions that satisfy each inequality. Then, find the intersection of all the regions to determine the solution to the system.
5. Using Technology to Graph Systems of Inequalities
Graphing calculators and computer software can be used to graph systems of inequalities. These tools can help you visualize the solution region and identify the boundary lines.
Common Challenges and Solutions
When solving systems of inequalities graphically, you may encounter several challenges. Here are some common issues and solutions:
- Challenge: The system has no solution.
- Solution: If the system has no solution, the graphs of the inequalities will not intersect, or the intersection will be empty.
- Challenge: The system has infinitely many solutions.
- Solution: If the system has infinitely many solutions, the graphs of the inequalities will coincide, or the intersection will be a region with no boundary lines.
In summary, solving systems of inequalities graphically involves graphing each inequality separately, identifying the solution region, and using test points to determine which side of a line satisfies an inequality. By following these steps, you can visualize and solve systems of linear and nonlinear inequalities.
The key to solving systems of inequalities graphically is to carefully graph each inequality and identify the regions that satisfy each inequality. With practice and patience, you can become proficient in solving systems of inequalities using graphical methods.
What is a system of inequalities?
+
A system of inequalities is a set of two or more inequalities that contain the same variables.
Why is graphical method useful for solving systems of inequalities?
+
Graphical method is useful for solving systems of inequalities because it allows us to visualize the solution region and identify the boundary lines.
How do I determine which side of a line satisfies an inequality?
+
To determine which side of a line satisfies an inequality, use a test point. Choose a point that is clearly on one side of the line and substitute the coordinates into the inequality.