Graphing Radical Functions Worksheet
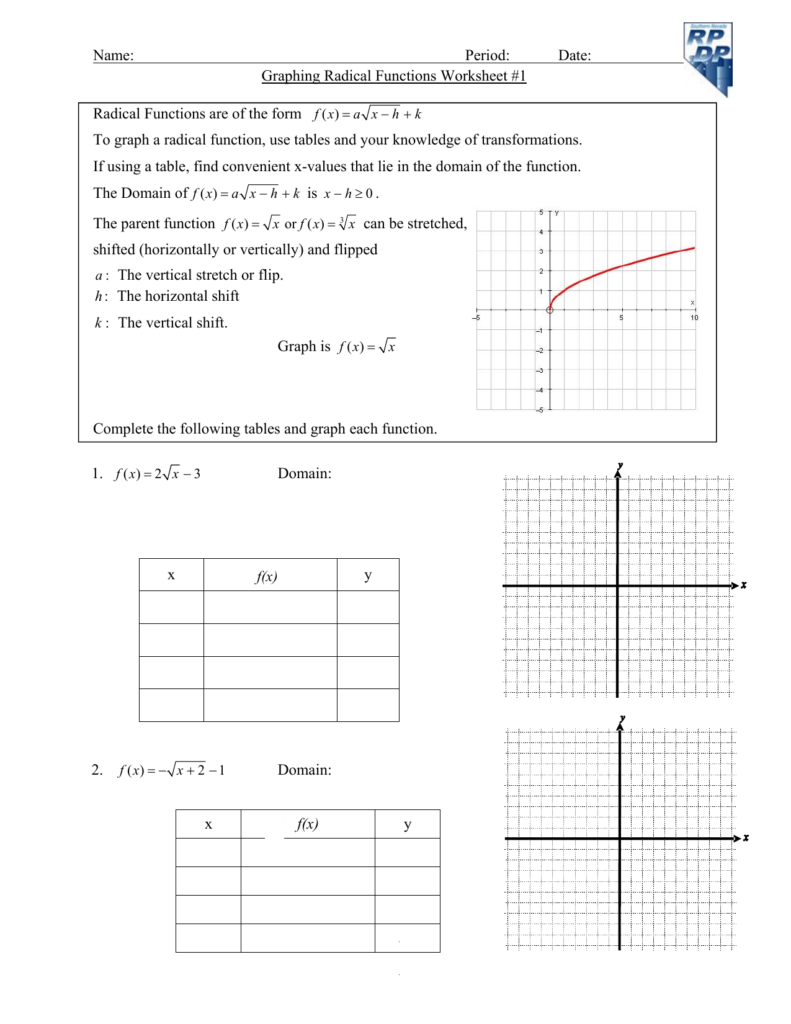
Graphing Radical Functions: A Comprehensive Guide
Radical functions are an essential part of algebra, and graphing them can be a challenging task. In this guide, we will walk you through the process of graphing radical functions, including square root, cube root, and nth root functions.
Understanding Radical Functions
Before we dive into graphing radical functions, it’s essential to understand what they are. Radical functions are functions that contain a radical, such as a square root or cube root, in the equation. The general form of a radical function is:
y = √(x) or y = ³√(x)
where y is the dependent variable, x is the independent variable, and √ or ³√ represents the radical.
Graphing Square Root Functions
Square root functions are the most common type of radical function. To graph a square root function, follow these steps:
- Identify the domain: The domain of a square root function is all real numbers greater than or equal to zero. This means that the graph will only exist in the first quadrant.
- Find the x-intercept: The x-intercept is the point where the graph intersects the x-axis. For a square root function, the x-intercept is always zero.
- Plot the points: Plot several points on the graph, making sure to include the x-intercept.
- Draw the curve: Draw a smooth curve through the points, making sure to keep the graph in the first quadrant.
Example: Graph the function y = √(x).

| x | y |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
Graph the points and draw a smooth curve to create the graph.
Graphing Cube Root Functions
Cube root functions are similar to square root functions, but with a few key differences. To graph a cube root function, follow these steps:
- Identify the domain: The domain of a cube root function is all real numbers.
- Find the x-intercept: The x-intercept is the point where the graph intersects the x-axis. For a cube root function, the x-intercept is always zero.
- Plot the points: Plot several points on the graph, making sure to include the x-intercept.
- Draw the curve: Draw a smooth curve through the points.
Example: Graph the function y = ³√(x).
| x | y |
|---|---|
| -1 | -1 |
| 0 | 0 |
| 1 | 1 |
| 8 | 2 |
Graph the points and draw a smooth curve to create the graph.
Graphing nth Root Functions
nth root functions are more complex than square root and cube root functions, but the process is similar. To graph an nth root function, follow these steps:
- Identify the domain: The domain of an nth root function is all real numbers greater than or equal to zero if n is even, and all real numbers if n is odd.
- Find the x-intercept: The x-intercept is the point where the graph intersects the x-axis. For an nth root function, the x-intercept is always zero.
- Plot the points: Plot several points on the graph, making sure to include the x-intercept.
- Draw the curve: Draw a smooth curve through the points.
Example: Graph the function y = ⁴√(x).
| x | y |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 16 | 2 |
| 81 | 3 |
Graph the points and draw a smooth curve to create the graph.
📝 Note: When graphing radical functions, it's essential to pay attention to the domain and range to ensure that the graph is accurate.
Practice Problems
Here are some practice problems to help you reinforce your understanding of graphing radical functions:
- Graph the function y = √(x + 1).
- Graph the function y = ³√(x - 2).
- Graph the function y = ⁵√(x + 3).
What is the domain of a square root function?
+The domain of a square root function is all real numbers greater than or equal to zero.
How do I graph a cube root function?
+To graph a cube root function, identify the domain, find the x-intercept, plot points, and draw a smooth curve through the points.
What is the difference between a square root function and a cube root function?
+The main difference is that a square root function has a domain of all real numbers greater than or equal to zero, while a cube root function has a domain of all real numbers.
Graphing radical functions requires attention to detail and an understanding of the domain and range. With practice, you’ll become proficient in graphing these functions and be able to apply your knowledge to more advanced math concepts.
Related Terms:
- Square root Functions Worksheet pdf
- Solving radical functions Worksheet
- Graphing Rational Functions Worksheet answer
- Graphing Cube Root Functions Worksheet
- Graphing reciprocal functions Worksheet
- Radical Functions review WORKSHEET