5 Ways to Master Graph Proportional Relationships
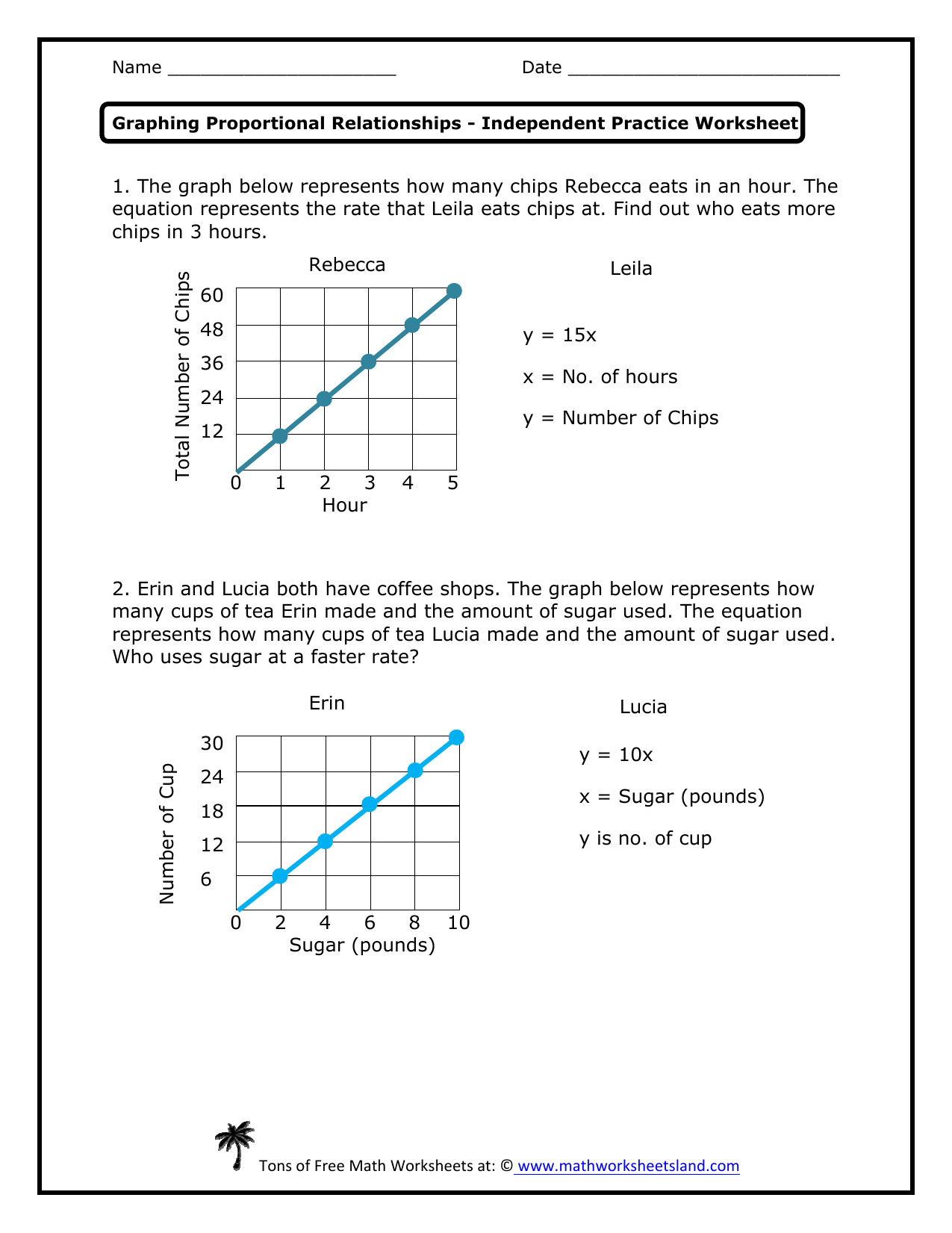
Understanding Graph Proportional Relationships
Graph proportional relationships are a fundamental concept in mathematics, particularly in algebra and geometry. They represent a linear relationship between two quantities, where one quantity is a constant multiple of the other. Mastering graph proportional relationships is crucial for solving various problems in mathematics, science, and real-life applications. In this article, we will explore five ways to master graph proportional relationships.
Method 1: Identifying Direct Proportional Relationships
Direct proportional relationships occur when the ratio of the dependent variable (y) to the independent variable (x) is constant. This can be represented by the equation y = kx, where k is the constant of proportionality.
- Example: A bakery sells 2 cookies for every 1 dollar. If we plot the number of cookies (y) against the amount of money (x), we get a straight line passing through the origin (0, 0). The constant of proportionality (k) is 2.
- Note: When identifying direct proportional relationships, look for a straight line passing through the origin with a constant slope.
📝 Note: The constant of proportionality (k) can be positive or negative, depending on the relationship.
Method 2: Identifying Inverse Proportional Relationships
Inverse proportional relationships occur when the product of the dependent variable (y) and the independent variable (x) is constant. This can be represented by the equation y = k/x, where k is the constant of proportionality.
- Example: A car travels 240 miles on 10 gallons of gas. If we plot the distance traveled (y) against the amount of gas consumed (x), we get a curve that approaches the x-axis as x increases. The constant of proportionality (k) is 240.
- Note: When identifying inverse proportional relationships, look for a curve that approaches the x-axis as x increases.
📊 Note: Inverse proportional relationships can be represented as a hyperbola on a graph.
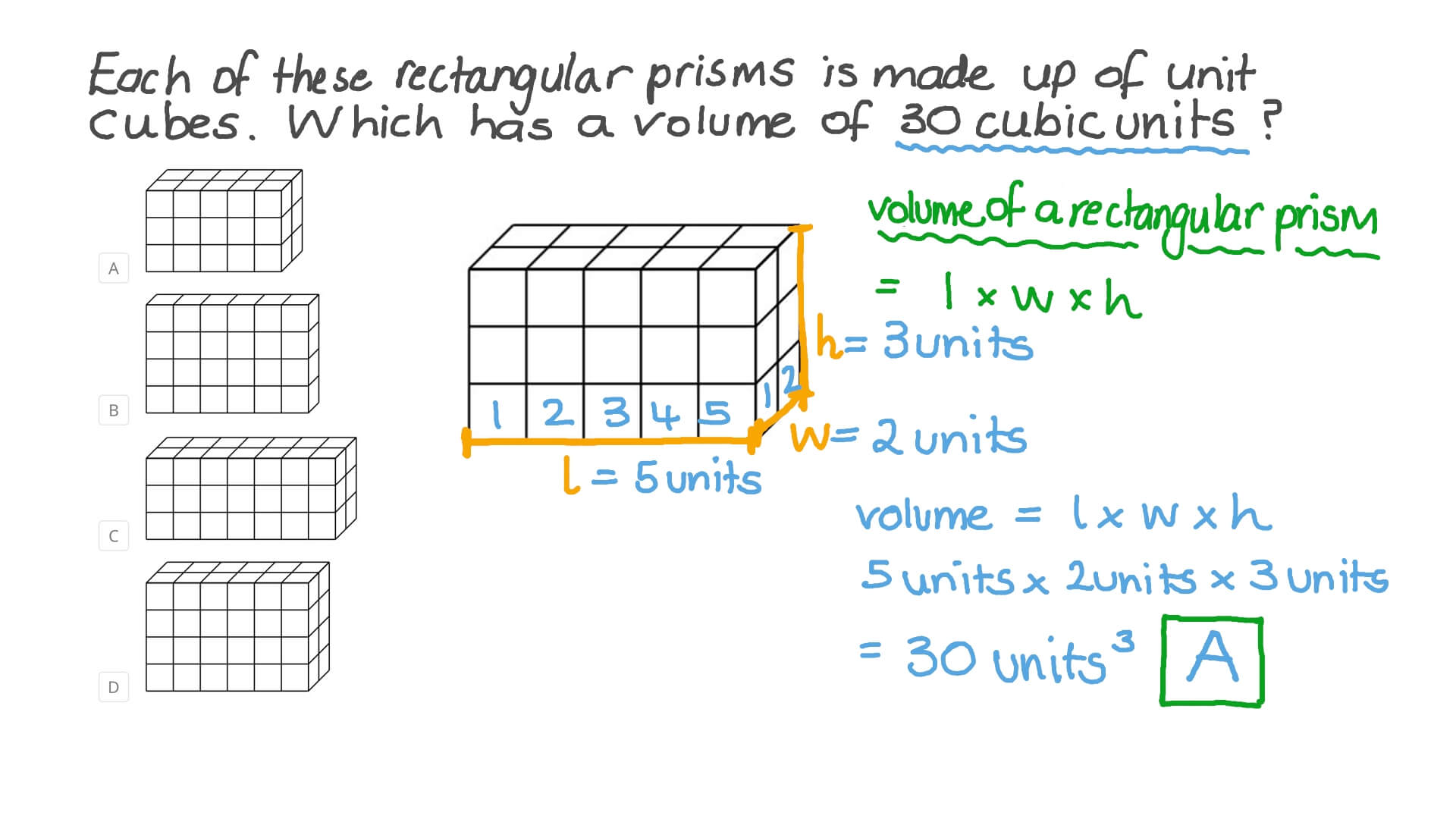
Method 3: Using Graphs to Represent Proportional Relationships
Graphs are a powerful tool for representing proportional relationships. By plotting the data on a coordinate plane, you can visualize the relationship between the variables.
- Example: A company sells 100 widgets for every 500 dollars. If we plot the number of widgets (y) against the amount of money (x), we get a straight line passing through the origin (0, 0). The constant of proportionality (k) is 0.2.
- Note: When using graphs to represent proportional relationships, make sure to label the axes and include a title.
| x (dollars) | y (widgets) |
|---|---|
| 500 | 100 |
| 1000 | 200 |
| 1500 | 300 |
Method 4: Writing Equations for Proportional Relationships
Once you have identified a proportional relationship, you can write an equation to represent it. The equation should be in the form y = kx for direct proportional relationships or y = k/x for inverse proportional relationships.
- Example: A bookshelf has 5 shelves, and each shelf can hold 8 books. If we plot the number of books (y) against the number of shelves (x), we get a straight line passing through the origin (0, 0). The constant of proportionality (k) is 8. The equation is y = 8x.
- Note: When writing equations for proportional relationships, make sure to include the constant of proportionality (k).
📝 Note: You can also write the equation in the form x = ky for inverse proportional relationships.
Method 5: Solving Problems Involving Proportional Relationships
Proportional relationships are used to solve a wide range of problems in mathematics, science, and real-life applications. By applying the concepts learned in this article, you can solve problems involving direct and inverse proportional relationships.
- Example: A water tank can hold 1000 liters of water. If 200 liters of water are already in the tank, and the water flows in at a rate of 10 liters per minute, how many minutes will it take to fill the tank?
- Solution: Let x be the number of minutes and y be the amount of water in the tank. The equation is y = 10x + 200. To find the time it takes to fill the tank, we need to find the value of x when y = 1000.
By applying the methods outlined in this article, you can master graph proportional relationships and solve a wide range of problems.
The concepts learned in this article can be applied to various real-life situations, such as understanding the relationship between the amount of money spent and the number of items purchased, or the relationship between the distance traveled and the amount of time taken.
In conclusion, graph proportional relationships are a fundamental concept in mathematics, and mastering them is crucial for solving various problems. By using the methods outlined in this article, you can identify direct and inverse proportional relationships, use graphs to represent proportional relationships, write equations for proportional relationships, and solve problems involving proportional relationships.
What is a proportional relationship?
+A proportional relationship is a linear relationship between two quantities, where one quantity is a constant multiple of the other.
How do I identify a direct proportional relationship?
+A direct proportional relationship can be identified by a straight line passing through the origin (0, 0) with a constant slope.
How do I write an equation for a proportional relationship?
+The equation for a proportional relationship should be in the form y = kx for direct proportional relationships or y = k/x for inverse proportional relationships.
Related Terms:
- teacher synergy llc
- IXL
- Khan Academy
- BrainPOP
- Udacity
- Duolingo