7 Essential Geometry Transformations to Master Now
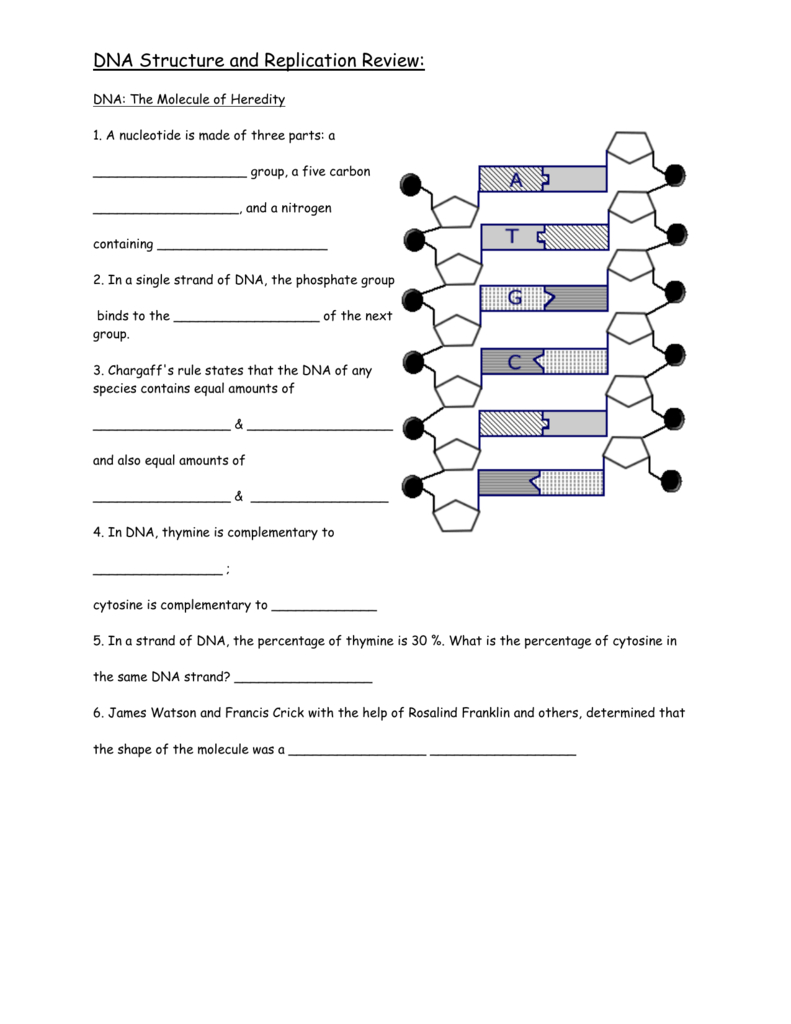
Mastering geometry transformations is a crucial skill for anyone interested in mathematics, science, engineering, and art. Geometry transformations are the building blocks of various mathematical concepts, including algebra, calculus, and computer graphics. In this article, we will explore 7 essential geometry transformations that you need to master now.
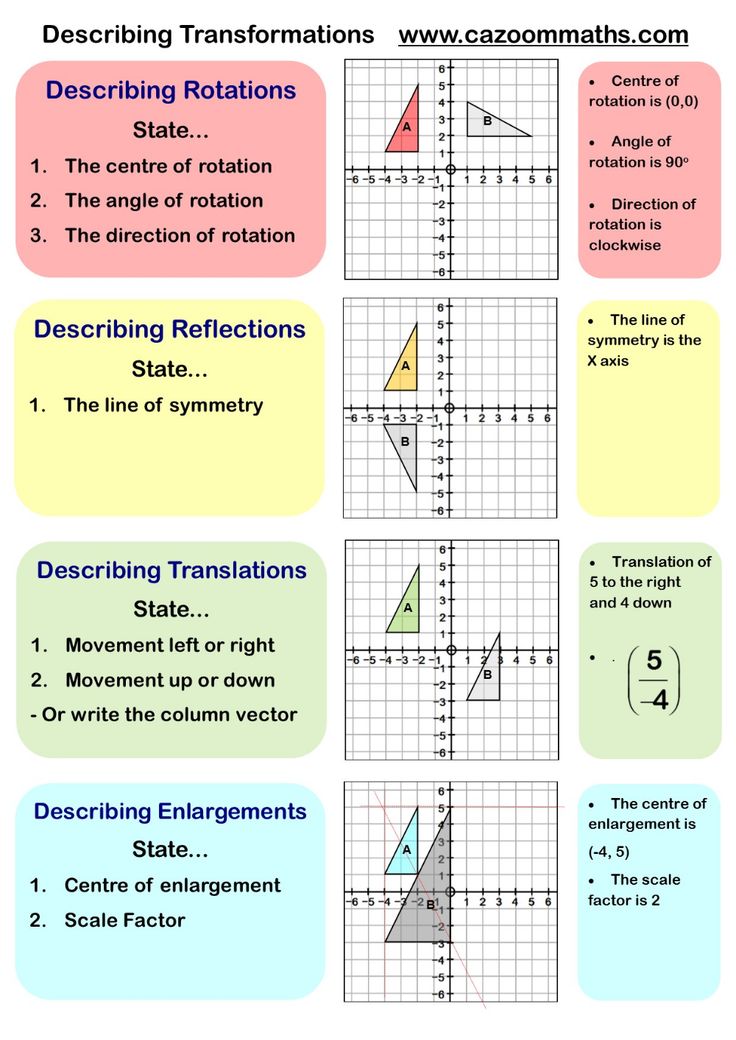
1. Translation
A translation is a transformation that moves a shape from one location to another without changing its size or orientation. It is like sliding a puzzle piece across a flat surface. To perform a translation, you need to know the distance and direction of the movement.
Example:

| Initial Point | Translated Point |
|---|---|
| (x, y) | (x + a, y + b) |
where (x, y) is the initial point, and (x + a, y + b) is the translated point.
2. Rotation
A rotation is a transformation that turns a shape around a fixed point, called the center of rotation. The shape remains the same size, but its orientation changes. To perform a rotation, you need to know the angle of rotation and the center of rotation.
Example:
| Initial Point | Rotated Point |
|---|---|
| (x, y) | (x cos θ - y sin θ, x sin θ + y cos θ) |
where (x, y) is the initial point, θ is the angle of rotation, and (x cos θ - y sin θ, x sin θ + y cos θ) is the rotated point.
3. Reflection
A reflection is a transformation that flips a shape over a line, called the line of reflection. The shape remains the same size, but its orientation changes. To perform a reflection, you need to know the line of reflection.
Example:
| Initial Point | Reflected Point |
|---|---|
| (x, y) | (2a - x, 2b - y) |
where (x, y) is the initial point, (a, b) is a point on the line of reflection, and (2a - x, 2b - y) is the reflected point.
4. Dilation
A dilation is a transformation that changes the size of a shape. The shape remains the same orientation, but its size changes. To perform a dilation, you need to know the scale factor.
Example:
| Initial Point | Dilated Point |
|---|---|
| (x, y) | (kx, ky) |
where (x, y) is the initial point, k is the scale factor, and (kx, ky) is the dilated point.
5. Glide Reflection
A glide reflection is a transformation that combines a reflection and a translation. It is like reflecting a shape over a line and then sliding it along that line.
Example:
| Initial Point | Glide Reflected Point |
|---|---|
| (x, y) | (2a - x + c, 2b - y + d) |
where (x, y) is the initial point, (a, b) is a point on the line of reflection, (c, d) is the translation vector, and (2a - x + c, 2b - y + d) is the glide reflected point.
6. Rotational Symmetry
Rotational symmetry is a transformation that turns a shape around a fixed point, called the center of rotation, by a certain angle. If the shape looks the same after a rotation, it is said to have rotational symmetry.
Example:
| Shape | Rotational Symmetry |
|---|---|
| Equilateral Triangle | 120°, 240°, 360° |
| Square | 90°, 180°, 270°, 360° |
7. Tessellations
A tessellation is a transformation that repeats a shape to cover a plane without overlapping or gaps. It is like creating a mosaic art piece using identical shapes.
Example:
| Shape | Tessellation |
|---|---|
| Square | Grid of Squares |
| Triangle | Triangular Mosaic |
📝 Note: Mastering these 7 essential geometry transformations will help you to better understand various mathematical concepts and solve problems in mathematics, science, engineering, and art.
In conclusion, geometry transformations are a fundamental concept in mathematics and have numerous applications in various fields. By mastering the 7 essential geometry transformations, you will develop a deeper understanding of mathematical concepts and improve your problem-solving skills.
What is the difference between a translation and a rotation?
+A translation is a transformation that moves a shape from one location to another without changing its size or orientation. A rotation is a transformation that turns a shape around a fixed point, called the center of rotation, without changing its size.
What is the formula for a dilation?
+The formula for a dilation is (x, y) → (kx, ky), where (x, y) is the initial point, k is the scale factor, and (kx, ky) is the dilated point.
What is an example of a tessellation?
+An example of a tessellation is a grid of squares, where identical squares are repeated to cover a plane without overlapping or gaps.