5 Ways to Master Fractions of a Set

Unlocking the Secrets of Fractions of a Set

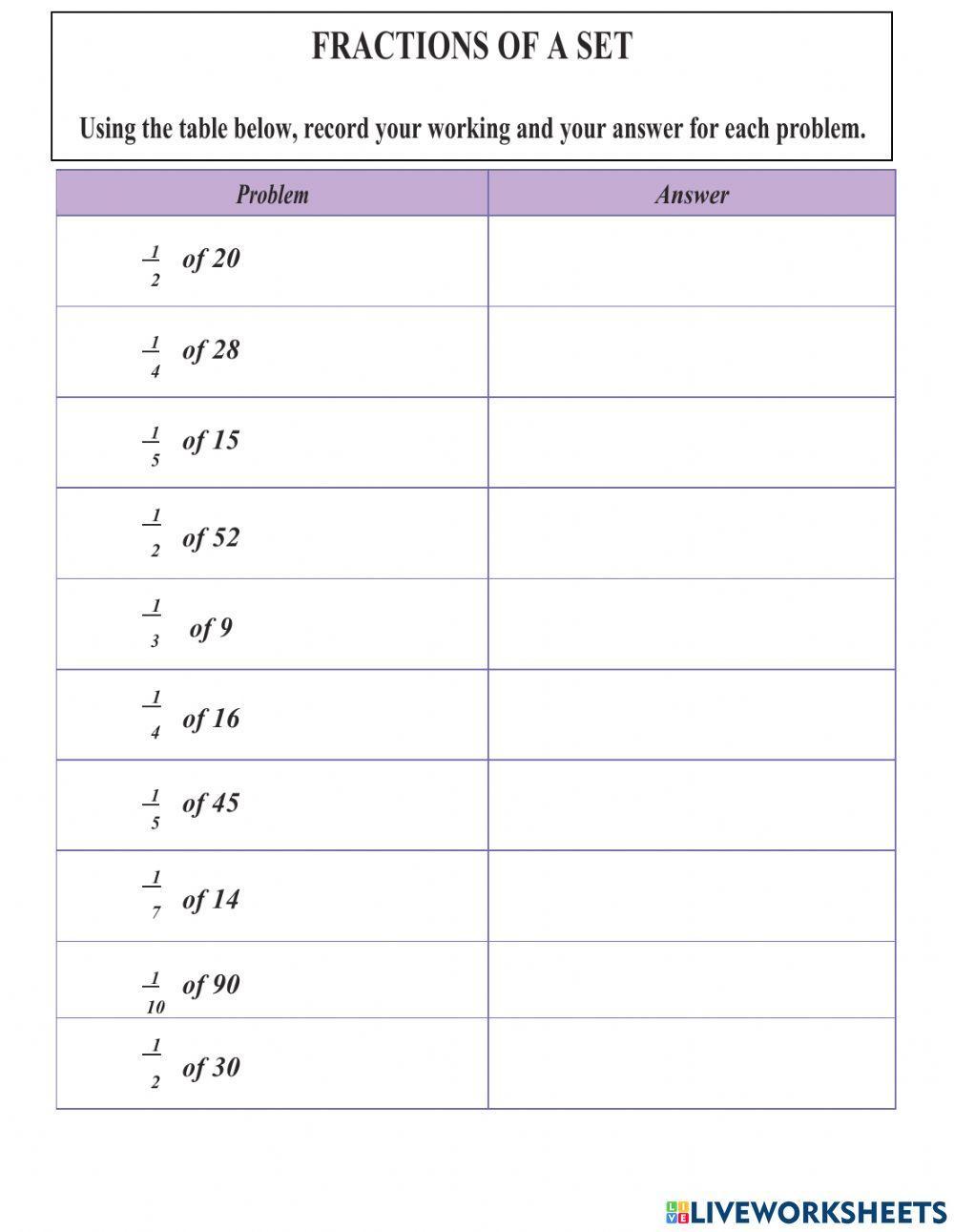
Fractions of a set are a fundamental concept in mathematics, and mastering them can unlock a world of problem-solving possibilities. Whether you’re a student looking to improve your math skills or a teacher seeking to help your students understand this concept, this article will provide you with 5 effective ways to master fractions of a set.

What are Fractions of a Set?

Before we dive into the ways to master fractions of a set, let’s first define what they are. A fraction of a set is a way to describe a part of a larger group or collection. It’s a way to show a proportion of the whole set. For example, if you have a set of 12 pencils and 3 of them are red, the fraction of red pencils is ³⁄₁₂ or ¹⁄₄.

1. Understanding the Concept of Equivalent Ratios

One of the key concepts to master when working with fractions of a set is equivalent ratios. Equivalent ratios are fractions that have the same value, but different numbers. For example, ¹⁄₂, ²⁄₄, and ³⁄₆ are all equivalent ratios. Understanding equivalent ratios will help you simplify fractions and make comparisons between different sets.

Example:

Simplify the fraction ⁶⁄₈.

🤔 Note: To simplify a fraction, divide both the numerator and denominator by the greatest common divisor (GCD). In this case, the GCD of 6 and 8 is 2.

Simplified fraction: ³⁄₄

2. Visualizing Fractions with Real-World Examples

Using real-world examples is an excellent way to visualize fractions of a set. This can help you understand the concept better and make it more relatable. For example, imagine you have a pizza that’s cut into 8 slices, and 3 of them are eaten. The fraction of the pizza that’s left is ⁵⁄₈.

Example:

A bookshelf has 12 books, and 4 of them are romance novels. What fraction of the books are romance novels?

Fraction: ⁴⁄₁₂ = ¹⁄₃

3. Practicing with Word Problems

Word problems are an excellent way to practice working with fractions of a set. They help you apply the concept to real-world scenarios and develop problem-solving skills. Here’s an example:

Example:

A bakery has 18 cupcakes, and 6 of them are chocolate. What fraction of the cupcakes are chocolate?

Fraction: ⁶⁄₁₈ = ¹⁄₃

4. Using Fractions to Compare Sets

Fractions of a set can be used to compare different sets. This is useful when you need to determine which set has a larger or smaller proportion of a particular item. For example, imagine you have two sets of pencils, and you want to know which set has a larger proportion of red pencils.

Example:

Set A has 12 pencils, and 4 of them are red. Set B has 18 pencils, and 6 of them are red. Which set has a larger proportion of red pencils?

Fraction of red pencils in Set A: ⁴⁄₁₂ = ¹⁄₃ Fraction of red pencils in Set B: ⁶⁄₁₈ = ¹⁄₃

Both sets have the same proportion of red pencils.

5. Creating Your Own Word Problems

Creating your own word problems is an excellent way to practice working with fractions of a set. This will help you develop problem-solving skills and apply the concept to different scenarios. Try creating word problems with different themes, such as food, animals, or objects.

Example:

Create a word problem using the theme of food.

Word problem: A restaurant has 20 tables, and 5 of them are reserved for a special event. What fraction of the tables are reserved?

Fraction: ⁵⁄₂₀ = ¹⁄₄

🤔 Note: Creating your own word problems will help you develop critical thinking skills and apply the concept of fractions of a set to different scenarios.

In conclusion, mastering fractions of a set requires practice, patience, and persistence. By understanding equivalent ratios, visualizing fractions with real-world examples, practicing with word problems, using fractions to compare sets, and creating your own word problems, you’ll become proficient in this fundamental math concept.