5 Ways to Simplify Fractions of a Fraction

What are Fractions of a Fraction?
Fractions of a fraction can be a complex and intimidating concept for many students. However, with the right approach, simplifying these types of fractions can become a straightforward process. In essence, a fraction of a fraction is a division of two fractions. To simplify these fractions, we need to multiply the numerator of the first fraction by the reciprocal of the second fraction.
Why Simplify Fractions of a Fraction?
Simplifying fractions of a fraction is essential in various mathematical operations, such as multiplication, division, and even algebra. When fractions are simplified, they become easier to work with and understand. Moreover, simplifying fractions can help avoid errors and make calculations more efficient.
Method 1: Multiply by the Reciprocal
One of the most common methods to simplify fractions of a fraction is to multiply the numerator of the first fraction by the reciprocal of the second fraction. This method is based on the concept that division is equivalent to multiplication by the reciprocal.
For example, let’s simplify the fraction: 1⁄2 ÷ 3⁄4
Multiply the numerator (1) by the reciprocal of the second fraction (4⁄3):
1 × 4⁄3 = 4⁄3
Divide the result by the denominator (2):
4⁄3 ÷ 2 = 4⁄6
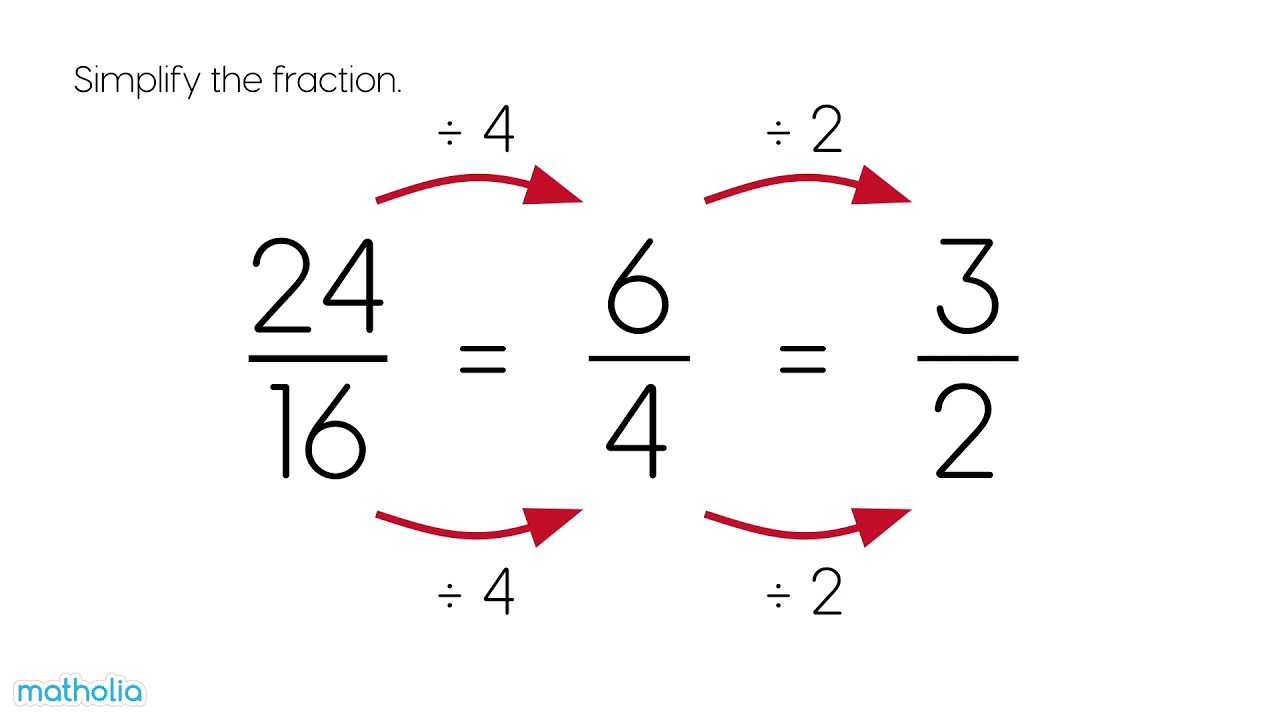
Simplify the fraction:
4⁄6 = 2⁄3
💡 Note: When multiplying fractions, make sure to multiply the numerators together and the denominators together.
Method 2: Use the Associative Property
Another method to simplify fractions of a fraction is to use the associative property of multiplication. This method involves multiplying the numerators together and the denominators together.
For example, let’s simplify the fraction: 2⁄3 × 3⁄4 ÷ 2⁄5
Multiply the numerators (2 × 3) and the denominators (3 × 4):
(2 × 3) / (3 × 4) = 6⁄12
Multiply the result by the reciprocal of the third fraction (5⁄2):
6⁄12 × 5⁄2 = 30⁄24
Simplify the fraction:
30⁄24 = 5⁄4
Method 3: Use a Common Denominator
Using a common denominator can also simplify fractions of a fraction. This method involves finding the least common multiple (LCM) of the denominators and then converting each fraction to have the LCM as the denominator.
For example, let’s simplify the fraction: 1⁄2 + 1⁄3 ÷ 2⁄5
Find the LCM of the denominators (2, 3, and 5):
LCM(2, 3, 5) = 30
Convert each fraction to have a denominator of 30:
1⁄2 = 15⁄30 1⁄3 = 10⁄30 2⁄5 = 12⁄30
Add and subtract the fractions:
(15⁄30 + 10⁄30) ÷ 12⁄30 = 25⁄30 ÷ 12⁄30
Multiply the numerators and denominators:
25 × 30⁄12 × 30 = 625⁄360
Simplify the fraction:
625⁄360 = 25⁄36
Method 4: Use a Variable
Using a variable can also simplify fractions of a fraction. This method involves assigning a variable to the fraction and then solving for the variable.
For example, let’s simplify the fraction: 2⁄3 ÷ 2⁄5
Let x be the result:
2⁄3 ÷ 2⁄5 = x
Multiply both sides by 2⁄5:
2⁄3 = x × 2⁄5
Multiply both sides by 3:
2 = x × 6⁄5
Divide both sides by 6⁄5:
x = 10⁄6
Simplify the fraction:
x = 5⁄3
Method 5: Use a Fraction Strip Diagram
Using a fraction strip diagram can also simplify fractions of a fraction. This method involves visualizing the fractions as strips and then comparing the strips to find the simplest form.
For example, let’s simplify the fraction: 1⁄2 ÷ 3⁄4
Draw a fraction strip diagram for 1⁄2 and 3⁄4:
1⁄2: □□□□ 3⁄4: □□□□
Compare the strips and find the simplest form:
1⁄2 ÷ 3⁄4 = 2⁄3
| Method | Description |
|---|---|
| Method 1: Multiply by the Reciprocal | Multiply the numerator by the reciprocal of the second fraction. |
| Method 2: Use the Associative Property | Multiply the numerators together and the denominators together. |
| Method 3: Use a Common Denominator | Find the least common multiple (LCM) of the denominators and convert each fraction to have the LCM as the denominator. |
| Method 4: Use a Variable | Assign a variable to the fraction and solve for the variable. |
| Method 5: Use a Fraction Strip Diagram | Visualize the fractions as strips and compare the strips to find the simplest form. |
In conclusion, simplifying fractions of a fraction can be a straightforward process using various methods. By mastering these methods, students can become more confident and proficient in simplifying complex fractions.