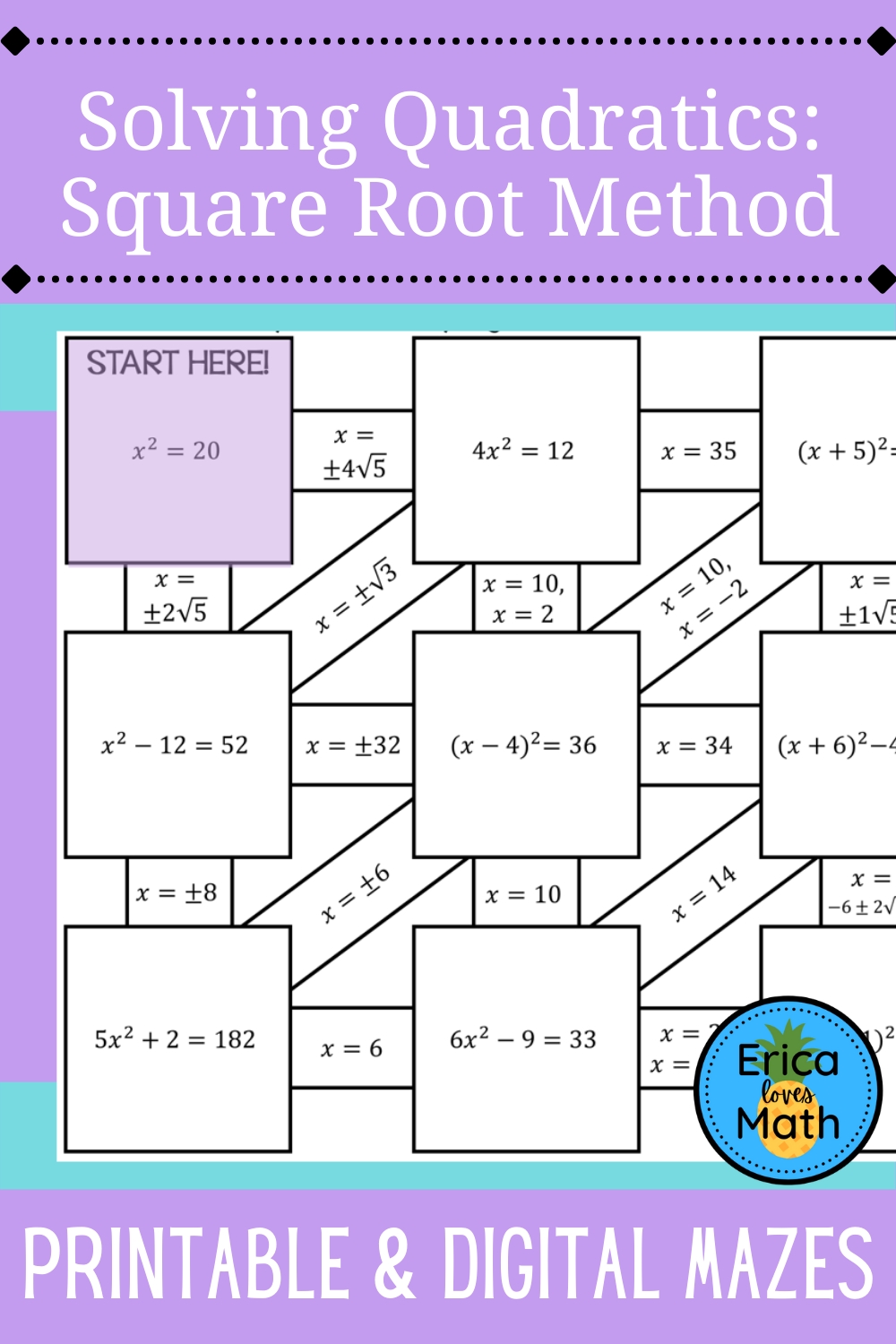
Mastering Quadratic Formula: Solve with Ease

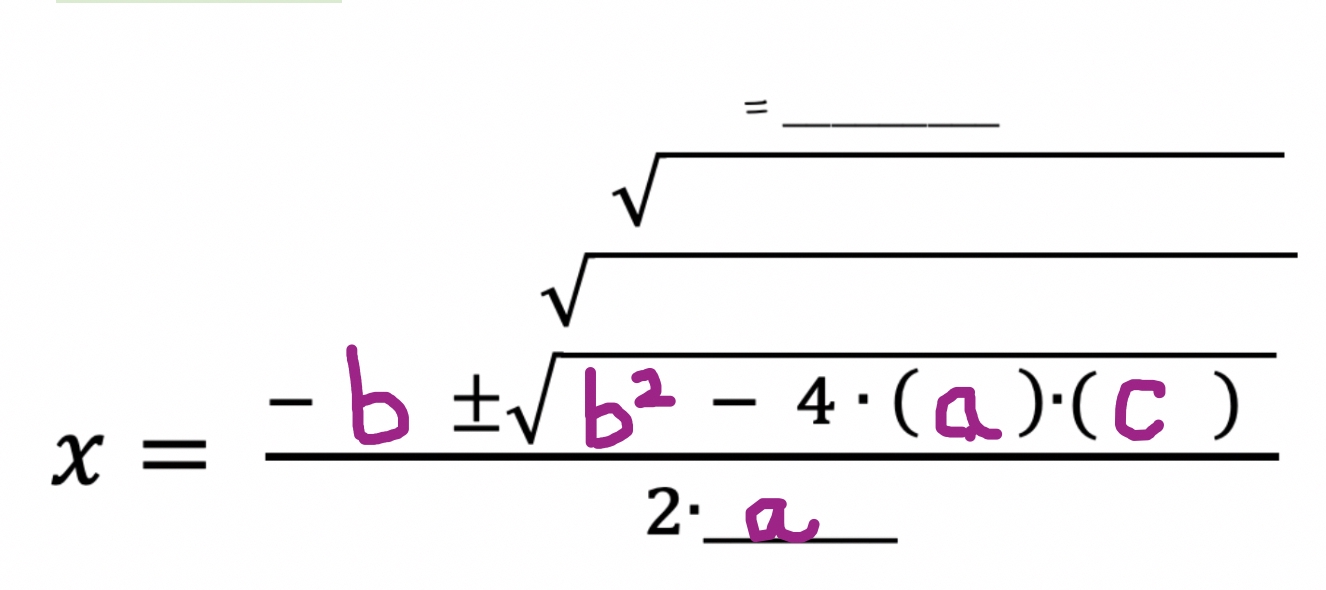
Unlocking the Secrets of the Quadratic Formula

The quadratic formula is a fundamental concept in algebra, used to solve quadratic equations of the form ax^2 + bx + c = 0. While it may seem daunting at first, with practice and patience, you can master the quadratic formula and solve equations with ease. In this article, we will delve into the world of quadratic equations, explore the formula in detail, and provide tips and tricks to help you become a pro at solving them.

Understanding Quadratic Equations

Before we dive into the quadratic formula, it’s essential to understand what a quadratic equation is. A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable (usually x) is two. The general form of a quadratic equation is:

ax^2 + bx + c = 0

where a, b, and c are constants, and x is the variable.

The Quadratic Formula

Now that we know what a quadratic equation is, let’s explore the quadratic formula. The quadratic formula is a mathematical formula that provides the solutions to a quadratic equation. The formula is:

x = (-b ± √(b^2 - 4ac)) / 2a

This formula may look complicated, but it’s actually quite simple once you understand what each part represents.

• x is the variable we are trying to solve for.
• a, b, and c are the coefficients of the quadratic equation.
• ± (plus-minus) indicates that there are two possible solutions.
• √ (square root) represents the square root of the expression inside the parentheses.

Breaking Down the Quadratic Formula

Let’s break down the quadratic formula into smaller parts to make it more manageable.

• -b: This is the negative of the coefficient of the x term.
• ±√(b^2 - 4ac): This is the square root of the discriminant, which is the expression inside the parentheses. The discriminant tells us whether the quadratic equation has two distinct solutions, one repeated solution, or no real solutions.
• / 2a: This is the denominator of the formula, which is twice the coefficient of the x^2 term.

How to Use the Quadratic Formula

Now that we understand the quadratic formula, let’s learn how to use it. Here are the steps:

1. Write down the quadratic equation: Start by writing down the quadratic equation you want to solve.
2. Identify the coefficients: Identify the coefficients a, b, and c in the quadratic equation.
3. Plug in the values: Plug in the values of a, b, and c into the quadratic formula.
4. Simplify the expression: Simplify the expression inside the square root (the discriminant).
5. Solve for x: Solve for x by adding or subtracting the square root of the discriminant to or from -b, and then dividing by 2a.

📝 Note: Make sure to simplify the expression inside the square root before solving for x.

Example: Solving a Quadratic Equation

Let’s use the quadratic formula to solve the equation x^2 + 5x + 6 = 0.

1. Write down the quadratic equation: x^2 + 5x + 6 = 0
2. Identify the coefficients: a = 1, b = 5, c = 6
3. Plug in the values: x = (-(5) ± √((5)^2 - 4(1)(6))) / 2(1)
4. Simplify the expression: x = (-5 ± √(25 - 24)) / 2
5. Solve for x: x = (-5 ± √1) / 2

Simplifying further, we get:

x = (-5 ± 1) / 2

x = -2 or x = -3

Tips and Tricks for Mastering the Quadratic Formula

Here are some tips and tricks to help you master the quadratic formula:

• Practice, practice, practice: The more you practice using the quadratic formula, the more comfortable you’ll become with it.
• Check your work: Always check your work by plugging your solutions back into the original equation.
• Use online resources: There are many online resources available to help you practice using the quadratic formula.
• Break down the formula: Break down the formula into smaller parts to make it more manageable.

Conclusion

Mastering the quadratic formula takes time and practice, but with patience and persistence, you can become a pro at solving quadratic equations. Remember to break down the formula into smaller parts, simplify the expression inside the square root, and always check your work. With these tips and tricks, you’ll be solving quadratic equations with ease in no time.