5 Easy Ways to Find Unit Rate

Finding unit rates is an essential skill in mathematics, particularly in real-world applications where comparisons and equivalencies are crucial. A unit rate is a ratio that compares two quantities where one of the quantities is 1. It helps us understand the price per unit, speed per hour, or any other rate that involves a quantity per unit of another quantity. Here are five easy ways to find unit rates:

Understanding Unit Rates

Before diving into the methods, it’s essential to grasp the concept of unit rates. A unit rate is a specific type of ratio where the second term is 1. For instance, if you can buy 3 apples for 1, the unit rate is 1 apple per 0.33. This helps you determine the cost of a single item from a given quantity.

Method 1: Simplifying Ratios

One of the simplest ways to find a unit rate is by simplifying a ratio. For example, if you have 12 pencils and they cost $3, you can find the unit rate by simplifying the ratio.

To simplify, divide both quantities by 12 (the quantity of pencils):

12 pencils ÷ 12 = 1 pencil 3 ÷ 12 = 0.25

Therefore, the unit rate is 1 pencil per $0.25.

Method 2: Using Division

Another straightforward method is using division. If you have a total cost and a total quantity, you can divide the cost by the quantity to find the unit rate.

For example, if 5 notebooks cost $10, you can find the unit rate by dividing the cost by the quantity:

10 ÷ 5 notebooks = 2 per notebook

Method 3: Using Proportional Reasoning

Sometimes, you might need to find a unit rate based on proportional reasoning. If you know the ratio of two quantities and one of the quantities is known, you can use proportional reasoning to find the unit rate.

For instance, if 3 cups of coffee cost $2 and you want to know the cost of 1 cup, you can use proportional reasoning:

3 cups ÷ 3 = 1 cup 2 ÷ 3 = 0.67 per cup

Therefore, the unit rate is 1 cup of coffee per $0.67.

Method 4: Converting Rates

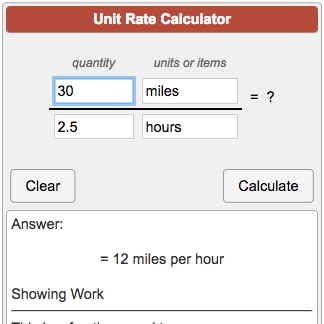
You can also convert rates to find unit rates. For example, if a car travels 240 miles in 4 hours, you can convert the rate to miles per hour by dividing the distance by the time:

240 miles ÷ 4 hours = 60 miles per hour

However, if you want to find the rate per minute, you can further convert the rate:

60 miles per hour ÷ 60 minutes per hour = 1 mile per minute

Method 5: Real-World Applications

Lastly, finding unit rates can be applied to real-world scenarios, such as comparing prices between stores or determining the best deal.

For example, if Store A sells 2 pounds of apples for 3 and Store B sells 3 pounds of apples for 4.50, you can find the unit rate to compare prices:

Store A: 3 ÷ 2 pounds = 1.50 per pound Store B: 4.50 ÷ 3 pounds = 1.50 per pound

Both stores have the same unit rate, but Store B offers a slightly better deal since you get an extra pound of apples for the same price.

📝 Note: When finding unit rates, make sure to check the units and ensure they match. This will help you avoid mistakes and provide accurate results.

To summarize, finding unit rates involves simplifying ratios, using division, applying proportional reasoning, converting rates, and using real-world applications. By mastering these methods, you’ll become proficient in calculating unit rates and making informed decisions in various aspects of life.