Finding Slope Worksheet With Answers
Understanding Slope and Its Importance in Mathematics
Slope is a fundamental concept in mathematics, particularly in algebra and geometry. It represents the ratio of the vertical change (rise) to the horizontal change (run) between two points on a line. Slope is crucial in understanding the steepness and direction of lines, which is essential in various fields like physics, engineering, economics, and more.
What is Slope?
Slope is a measure of how steep a line is and can be calculated using the following formula:
Slope (m) = Rise / Run
where:
- Rise is the vertical distance between two points on a line.
- Run is the horizontal distance between the same two points.
Types of Slope
There are several types of slope, including:
- Positive Slope: A line with a positive slope rises from left to right. The slope value is greater than 0.
- Negative Slope: A line with a negative slope falls from left to right. The slope value is less than 0.
- Zero Slope: A line with a zero slope is horizontal and has no rise.
- Undefined Slope: A line with an undefined slope is vertical and has no run.
Calculating Slope
To calculate the slope of a line, you need to know the coordinates of two points on the line. Use the formula:
m = (y2 - y1) / (x2 - x1)
where:
- (x1, y1) and (x2, y2) are the coordinates of the two points.
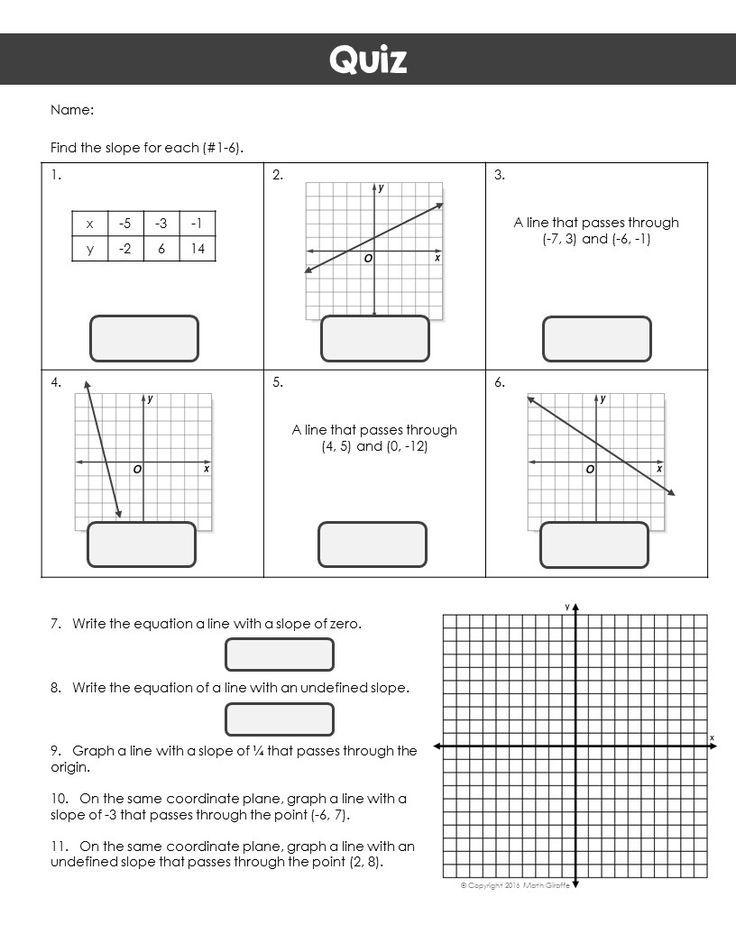
Slope Worksheet
Practice calculating slope with the following worksheet:
| Points | Slope |
|---|---|
| (2, 3) and (4, 5) | ? |
| (1, 2) and (3, 4) | ? |
| (0, 1) and (2, 3) | ? |
| (-1, 2) and (1, 4) | ? |
| (3, 2) and (5, 6) | ? |
Answers:
- m = (5 - 3) / (4 - 2) = 2 / 2 = 1
- m = (4 - 2) / (3 - 1) = 2 / 2 = 1
- m = (3 - 1) / (2 - 0) = 2 / 2 = 1
- m = (4 - 2) / (1 - (-1)) = 2 / 2 = 1
- m = (6 - 2) / (5 - 3) = 4 / 2 = 2
Additional Practice
Try calculating the slope of the following lines:
- A line passing through points (1, 3) and (2, 5)
- A line passing through points (-2, 1) and (0, 3)
- A line passing through points (2, 2) and (4, 6)
Important Notes
📝 Note: Always check if the line is horizontal or vertical before calculating the slope.
📝 Note: Make sure to use the correct formula when calculating slope.
The concept of slope is essential in mathematics and has numerous applications in various fields. By understanding how to calculate slope, you can analyze and visualize data more effectively. Remember to practice regularly to become proficient in calculating slope.
And that’s a wrap!
What is the formula for calculating slope?
+The formula for calculating slope is m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the coordinates of two points on the line.
What is the difference between positive and negative slope?
+A line with a positive slope rises from left to right, while a line with a negative slope falls from left to right.
How do I know if a line is horizontal or vertical?
+A line is horizontal if it has a zero slope, and it is vertical if it has an undefined slope.