5 Ways to Master Parallel Lines Cut by a Transversal
Understanding the Concept of Parallel Lines Cut by a Transversal
Parallel lines cut by a transversal is a fundamental concept in geometry that deals with the properties of lines and angles. When two parallel lines are cut by a transversal, it creates several angles that have specific relationships with each other. Mastering this concept is crucial for solving various problems in geometry and is a building block for more advanced topics.
1. Learn the Basic Properties of Parallel Lines Cut by a Transversal
To start mastering parallel lines cut by a transversal, it’s essential to learn the basic properties of this concept. Here are some key properties to remember:
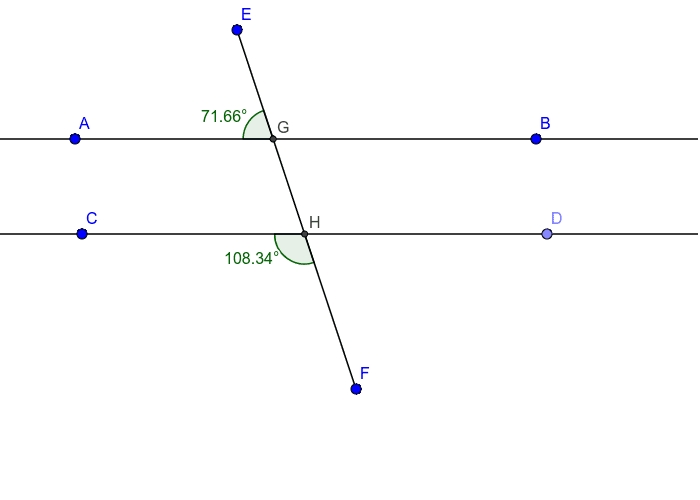
- Corresponding Angles: When two parallel lines are cut by a transversal, the corresponding angles are equal. For example, ∠1 = ∠5 and ∠2 = ∠6.
- Alternate Interior Angles: The alternate interior angles are also equal. For example, ∠3 = ∠5 and ∠4 = ∠6.
- Alternate Exterior Angles: The alternate exterior angles are equal as well. For example, ∠1 = ∠7 and ∠2 = ∠8.
- Interior Angles on the Same Side of the Transversal: The interior angles on the same side of the transversal are supplementary (add up to 180 degrees). For example, ∠3 + ∠5 = 180 degrees.
🔍 Note: Understanding these properties is crucial for solving problems related to parallel lines cut by a transversal.
2. Practice Identifying Angles and Relationships
Once you have a grasp of the basic properties, practice identifying angles and their relationships. Here’s an example:
Given the diagram below, identify the corresponding angles, alternate interior angles, and alternate exterior angles.
| Angle | Measurement |
|---|---|
| ∠1 | 60 degrees |
| ∠2 | 120 degrees |
| ∠3 | ? |
| ∠4 | ? |
| ∠5 | ? |
| ∠6 | ? |
| ∠7 | ? |
| ∠8 | ? |
Using the properties of parallel lines cut by a transversal, we can identify the following relationships:
- ∠1 = ∠5 = 60 degrees (corresponding angles)
- ∠2 = ∠6 = 120 degrees (corresponding angles)
- ∠3 = ∠5 = 60 degrees (alternate interior angles)
- ∠4 = ∠6 = 120 degrees (alternate interior angles)
- ∠1 = ∠7 = 60 degrees (alternate exterior angles)
- ∠2 = ∠8 = 120 degrees (alternate exterior angles)
3. Solve Problems Using the Properties of Parallel Lines Cut by a Transversal
Now that you have a good understanding of the properties and can identify angles and relationships, practice solving problems. Here’s an example:
Problem: In the diagram below, if ∠1 = 30 degrees, find the measurement of ∠5.
Using the properties of parallel lines cut by a transversal, we can identify the corresponding angles: ∠1 = ∠5. Since ∠1 = 30 degrees, we can conclude that ∠5 = 30 degrees as well.
📝 Note: Practice solving various problems to become more proficient in using the properties of parallel lines cut by a transversal.
4. Use Real-World Examples to Reinforce Understanding
To make the concept more engaging and relevant, use real-world examples to reinforce understanding. Here’s an example:
Example: Railroad tracks are an example of parallel lines cut by a transversal. The rails are parallel to each other, and the ties that connect them form a transversal. The angles formed by the rails and ties demonstrate the properties of parallel lines cut by a transversal.
5. Review and Reflect on the Concept Regularly
Finally, review and reflect on the concept of parallel lines cut by a transversal regularly. Here are some tips:
- Review the properties and relationships regularly.
- Practice solving problems and identifying angles and relationships.
- Use real-world examples to reinforce understanding.
- Reflect on what you’ve learned and what you need to work on.
By following these steps, you’ll become proficient in mastering parallel lines cut by a transversal and be able to apply this concept to various problems in geometry.
In summary, mastering parallel lines cut by a transversal requires a combination of understanding the basic properties, practicing identification and problem-solving, using real-world examples, and regular review and reflection. By following these steps, you’ll become proficient in this fundamental concept and be able to tackle more advanced topics in geometry.
What are corresponding angles in parallel lines cut by a transversal?
+Corresponding angles are angles that are in the same relative position on each line, such as ∠1 and ∠5.
What is the relationship between alternate interior angles in parallel lines cut by a transversal?
+Alternate interior angles are equal, such as ∠3 and ∠5.
How can I practice solving problems related to parallel lines cut by a transversal?
+You can practice solving problems by using online resources, such as worksheets and quizzes, or by creating your own problems using diagrams and measurements.



