5 Ways to Find Equivalent Fractions
Understanding Equivalent Fractions
Equivalent fractions are fractions that represent the same value, even if their numerators and denominators are different. For instance, 1⁄2, 2⁄4, and 3⁄6 are all equivalent fractions. Finding equivalent fractions is a crucial skill in mathematics, as it helps in simplifying complex fractions, comparing fractions, and solving equations. In this article, we will explore five ways to find equivalent fractions.
Method 1: Multiplying Numerator and Denominator by the Same Number
One way to find equivalent fractions is by multiplying both the numerator and the denominator by the same number. This method does not change the value of the fraction. For example, to find an equivalent fraction of 3⁄4, we can multiply both the numerator and the denominator by 2.
🤔 Note: When multiplying the numerator and denominator by the same number, the resulting fraction will have the same value as the original fraction.

| Original Fraction | Multiply by | Equivalent Fraction |
|---|---|---|
| 3/4 | 2 | 6/8 |
| 1/2 | 3 | 3/6 |
Method 2: Dividing Numerator and Denominator by the Same Number
Another way to find equivalent fractions is by dividing both the numerator and the denominator by the same number. This method also does not change the value of the fraction. For example, to find an equivalent fraction of 12⁄16, we can divide both the numerator and the denominator by 4.
🤔 Note: When dividing the numerator and denominator by the same number, the resulting fraction will have the same value as the original fraction.
| Original Fraction | Divide by | Equivalent Fraction |
|---|---|---|
| 12/16 | 4 | 3/4 |
| 6/12 | 2 | 3/6 |
Method 3: Simplifying Fractions
Simplifying fractions is another way to find equivalent fractions. To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and the denominator and divide both numbers by the GCD. For example, to simplify the fraction 8⁄12, we need to find the GCD of 8 and 12, which is 4.
🤔 Note: Simplifying fractions can help reduce the fraction to its simplest form, making it easier to compare and solve equations.
| Original Fraction | GCD | Equivalent Fraction |
|---|---|---|
| 8/12 | 4 | 2/3 |
| 6/8 | 2 | 3/4 |
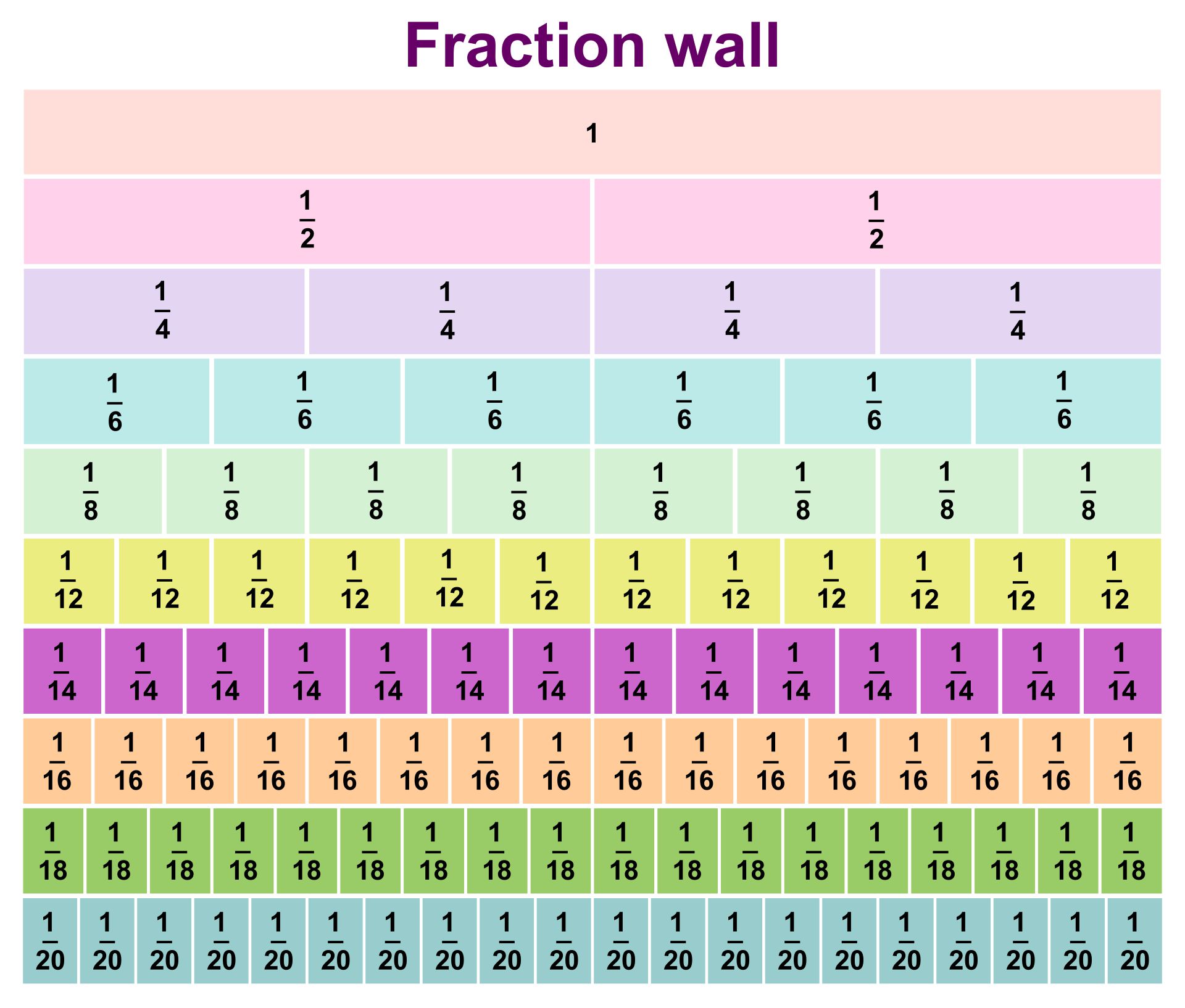
Method 4: Using Visual Models
Visual models can also be used to find equivalent fractions. For example, we can use a number line or a fraction strip to compare fractions and find equivalent fractions. Visual models can help students understand the concept of equivalent fractions and make it easier to compare fractions.
🤔 Note: Visual models can be a powerful tool in helping students understand complex mathematical concepts, including equivalent fractions.
Method 5: Using Real-World Examples
Real-world examples can also be used to find equivalent fractions. For instance, we can use measurement units, such as inches and feet, to find equivalent fractions. For example, 1⁄2 inch is equivalent to 6⁄12 inches.
🤔 Note: Real-world examples can help make mathematical concepts more relatable and easier to understand.
In conclusion, there are several ways to find equivalent fractions, including multiplying numerator and denominator by the same number, dividing numerator and denominator by the same number, simplifying fractions, using visual models, and using real-world examples. Understanding equivalent fractions is essential in mathematics, as it helps in simplifying complex fractions, comparing fractions, and solving equations.
What are equivalent fractions?
+Equivalent fractions are fractions that represent the same value, even if their numerators and denominators are different.
How can we find equivalent fractions?
+We can find equivalent fractions by multiplying numerator and denominator by the same number, dividing numerator and denominator by the same number, simplifying fractions, using visual models, and using real-world examples.
Why is understanding equivalent fractions important in mathematics?
+Understanding equivalent fractions is essential in mathematics, as it helps in simplifying complex fractions, comparing fractions, and solving equations.



