5 Essential Exponent Rules to Master

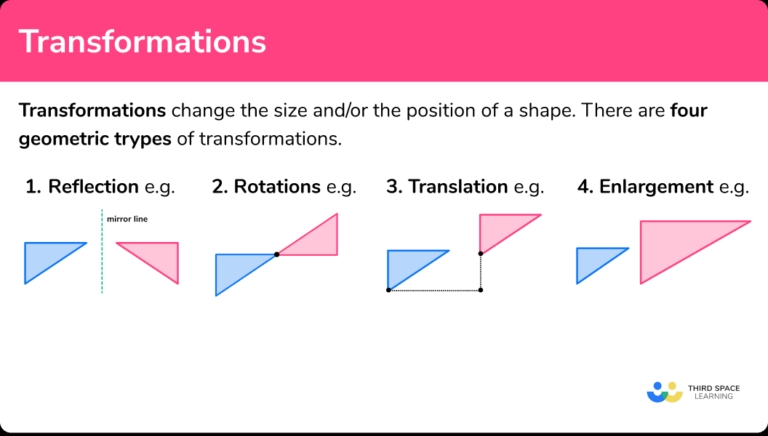
Exponent Rules: The Foundation of Algebra and Beyond
Exponents are a fundamental concept in mathematics, and mastering their rules is crucial for success in algebra, geometry, and various branches of mathematics. In this article, we will delve into five essential exponent rules that you need to master. These rules will help you simplify complex expressions, solve equations, and tackle advanced mathematical concepts with confidence.
Rule 1: The Product of Powers Rule
The product of powers rule states that when you multiply two powers with the same base, you add their exponents. Mathematically, this can be represented as:
a^m × a^n = a^(m+n)
For example:
2^3 × 2^4 = 2^(3+4) = 2^7
This rule applies to any base, not just numbers. For instance:
x^2 × x^5 = x^(2+5) = x^7
🤔 Note: The product of powers rule only applies when the bases are the same. If the bases are different, you cannot combine the exponents.
Rule 2: The Quotient of Powers Rule
The quotient of powers rule states that when you divide two powers with the same base, you subtract their exponents. Mathematically, this can be represented as:
a^m ÷ a^n = a^(m-n)
For example:
2^7 ÷ 2^4 = 2^(7-4) = 2^3
This rule applies to any base, not just numbers. For instance:
x^8 ÷ x^3 = x^(8-3) = x^5
🤔 Note: The quotient of powers rule only applies when the bases are the same. If the bases are different, you cannot combine the exponents.
Rule 3: The Power of a Power Rule
The power of a power rule states that when you raise a power to another power, you multiply the exponents. Mathematically, this can be represented as:
(a^m)^n = a^(m×n)
For example:
(2^3)^4 = 2^(3×4) = 2^12
This rule applies to any base, not just numbers. For instance:
(x^2)^5 = x^(2×5) = x^10
🤔 Note: The power of a power rule applies to any base, not just numbers.
Rule 4: The Power of a Product Rule
The power of a product rule states that when you raise a product to a power, you raise each factor to that power. Mathematically, this can be represented as:
(ab)^n = a^n × b^n
For example:
(2 × 3)^4 = 2^4 × 3^4
This rule applies to any base, not just numbers. For instance:
(xy)^5 = x^5 × y^5
🤔 Note: The power of a product rule applies to any base, not just numbers.
Rule 5: The Zero Exponent Rule
The zero exponent rule states that any base raised to the power of zero is equal to 1. Mathematically, this can be represented as:
a^0 = 1
For example:
2^0 = 1
This rule applies to any base, not just numbers. For instance:
x^0 = 1
🤔 Note: The zero exponent rule applies to any base, not just numbers.
In conclusion, mastering these five essential exponent rules will help you simplify complex expressions, solve equations, and tackle advanced mathematical concepts with confidence. Remember to apply these rules carefully, and don’t hesitate to practice until you feel comfortable using them.
What is the product of powers rule?
+
The product of powers rule states that when you multiply two powers with the same base, you add their exponents.
What is the quotient of powers rule?
+
The quotient of powers rule states that when you divide two powers with the same base, you subtract their exponents.
What is the power of a power rule?
+
The power of a power rule states that when you raise a power to another power, you multiply the exponents.