Transform Your Math Skills with Sequence of Transformations

Unlocking the Power of Transformations in Math

Transformations are a fundamental concept in mathematics, and mastering them can elevate your math skills to the next level. In this article, we will delve into the world of transformations, exploring what they are, how they work, and how to apply them to solve problems. By the end of this journey, you will be equipped with the knowledge and skills to transform your math abilities.

What are Transformations?

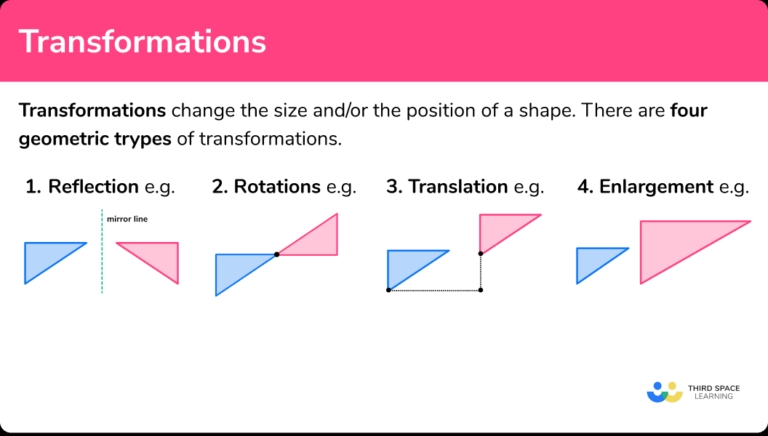
In mathematics, a transformation is a way of changing a shape or a function while preserving its essential properties. There are four main types of transformations:

• Translation: Moving a shape from one location to another without changing its size or orientation.
• Rotation: Turning a shape around a fixed point without changing its size.
• Reflection: Flipping a shape over a line or a plane without changing its size.
• Dilation: Enlarging or reducing a shape without changing its orientation.

Each of these transformations can be applied individually or in combination to create a wide range of effects.

Sequence of Transformations

A sequence of transformations is a series of transformations applied one after the other. This can be represented using a notation system, such as:

T1 (T2 (T3 ( shape ))))

Where T1, T2, and T3 are individual transformations, and the shape is the original object being transformed.

For example, consider a rectangle that undergoes a translation, followed by a rotation, and finally a reflection. The sequence of transformations would be:

Translation ( Rotation ( Reflection ( rectangle ))))

Key Concepts to Understand

Before diving deeper into the world of transformations, it’s essential to grasp the following key concepts:

• Coordinate plane: A two-dimensional grid used to represent points and shapes.
• Vectors: Quantities with both magnitude and direction, used to describe translations and rotations.
• Angles: Measured in degrees, used to describe rotations and reflections.
• Center of rotation: The fixed point around which a shape rotates.

Applying Transformations

Transformations can be applied in various ways, depending on the problem. Here are some common methods:

• Graphical method: Using a coordinate plane to visualize and apply transformations.
• Algebraic method: Using equations and formulas to represent and apply transformations.
• Geometric method: Using shapes and geometric properties to apply transformations.

💡 Note: The choice of method depends on the specific problem and the level of complexity.

Real-World Applications

Transformations have numerous real-world applications, including:

• Computer graphics: Transformations are used to create 3D models, animations, and special effects.
• Architecture: Transformations are used to design buildings, bridges, and other structures.
• Physics: Transformations are used to describe the motion of objects and the behavior of forces.

Common Challenges and Solutions

When working with transformations, you may encounter common challenges, such as:

• Difficulty visualizing transformations: Use graphical methods or online tools to help visualize transformations.
• Trouble applying multiple transformations: Break down the sequence of transformations into individual steps, and apply each one separately.
• Confusion between similar transformations: Use the notation system to keep track of transformations, and review the definitions of each type.

Conclusion

Transformations are a powerful tool in mathematics, allowing you to manipulate shapes and functions in a wide range of ways. By understanding the different types of transformations, mastering the notation system, and practicing with real-world applications, you can transform your math skills and unlock new levels of problem-solving abilities.

Related Terms:

• teacher synergy llc
• Khan Academy
• IXL
• BrainPOP
• Udacity
• Duolingo