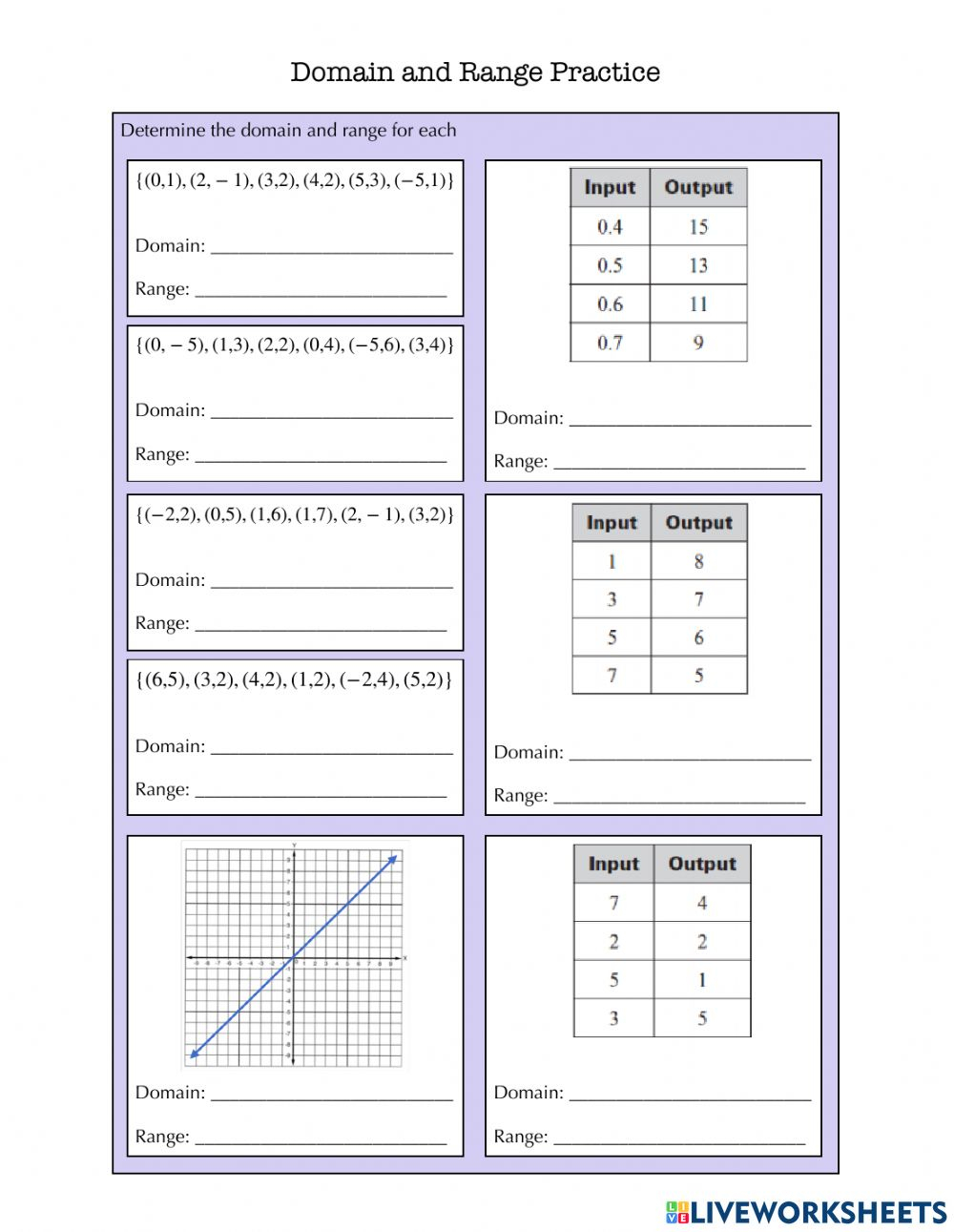
Domain And Range Worksheet
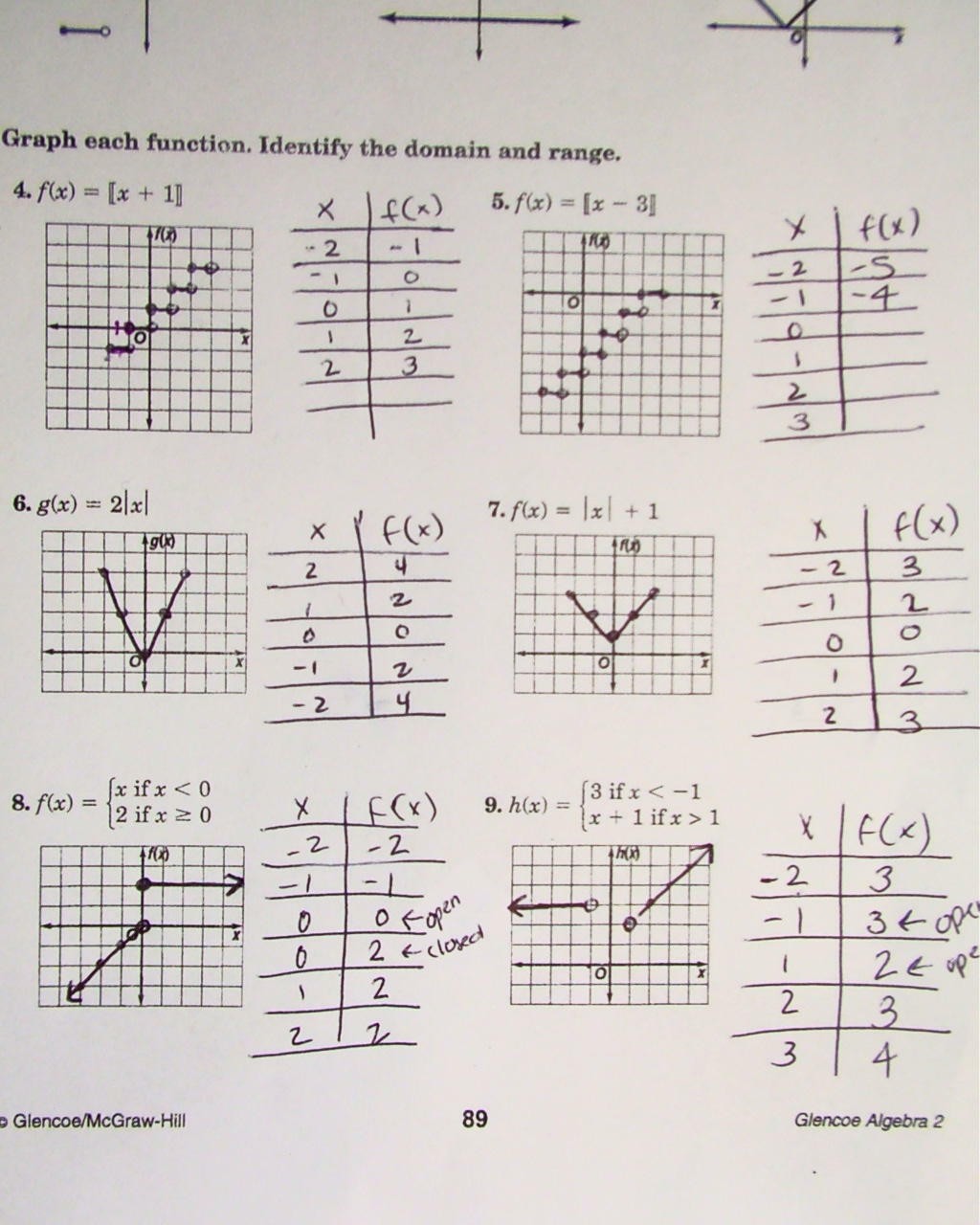
Understanding Domain and Range: A Comprehensive Guide
When working with functions, it’s essential to understand the concepts of domain and range. These two fundamental concepts in mathematics help you determine the input and output values of a function. In this article, we’ll delve into the world of domain and range, providing you with a comprehensive guide to help you grasp these concepts.
What is Domain?
The domain of a function is the set of all possible input values for which the function is defined. In other words, it’s the set of all values that you can plug into the function without getting an undefined result. For example, consider the function f(x) = 1/x. The domain of this function is all real numbers except x = 0, since division by zero is undefined.
What is Range?
The range of a function, on the other hand, is the set of all possible output values that the function can produce. It’s the set of all values that you can get as a result of plugging in different input values into the function. Using the same example as above, the range of the function f(x) = 1/x is all real numbers except y = 0, since the function will never produce a result of 0.
How to Find Domain and Range
Finding the domain and range of a function can be a straightforward process if you know the right steps to follow. Here’s a step-by-step guide to help you find the domain and range of a function:
- Identify the type of function you’re working with. Is it a linear function, a quadratic function, or a rational function?
- Look for any restrictions on the domain, such as division by zero or square roots of negative numbers.
- Use algebraic techniques, such as solving equations and inequalities, to find the domain and range.
- Graph the function to visualize the domain and range.
Example 1: Finding Domain and Range of a Linear Function
Consider the linear function f(x) = 2x + 3. To find the domain and range, follow these steps:
- Identify the type of function: linear function
- Look for restrictions on the domain: none
- Use algebraic techniques: the function is defined for all real numbers
- Graph the function: the graph is a straight line
Domain: all real numbers Range: all real numbers
Example 2: Finding Domain and Range of a Quadratic Function
Consider the quadratic function f(x) = x^2 + 4x + 4. To find the domain and range, follow these steps:
- Identify the type of function: quadratic function
- Look for restrictions on the domain: none
- Use algebraic techniques: factor the quadratic expression to find the vertex
- Graph the function: the graph is a parabola that opens upward
Domain: all real numbers Range: all real numbers greater than or equal to 0
Worksheet: Domain and Range
Now that you’ve learned the basics of domain and range, it’s time to practice! Try solving the following problems:
| Function | Domain | Range |
|---|---|---|
| f(x) = 1/x | ||
| f(x) = x^2 + 2x + 1 | ||
| f(x) = 3x - 2 | ||
| f(x) = x^3 - 2x^2 - 5x + 1 |
| Function | Domain | Range |
|---|---|---|
| f(x) = 1/x | x ≠ 0 | y ≠ 0 |
| f(x) = x^2 + 2x + 1 | all real numbers | y ≥ 0 |
| f(x) = 3x - 2 | all real numbers | all real numbers |
| f(x) = x^3 - 2x^2 - 5x + 1 | all real numbers | all real numbers |
📝 Note: Remember to check your work by plugging in different input values to ensure that your domain and range are correct.
Now that you’ve practiced finding the domain and range of different functions, you should have a better understanding of these fundamental concepts. Remember to always check your work and use algebraic techniques to find the domain and range of a function.
What is the difference between domain and range?
+The domain of a function is the set of all possible input values, while the range is the set of all possible output values.
How do I find the domain and range of a function?
+Identify the type of function, look for restrictions on the domain, use algebraic techniques, and graph the function to find the domain and range.
What is an example of a function with a restricted domain?
+The function f(x) = 1/x has a restricted domain, since division by zero is undefined.
To summarize, understanding domain and range is crucial for working with functions. By following the steps outlined in this guide, you’ll be able to find the domain and range of different types of functions. Remember to always check your work and use algebraic techniques to ensure accuracy. With practice, you’ll become proficient in finding the domain and range of functions, and you’ll be well on your way to mastering mathematics.