5 Ways to Solve Absolute Value Inequalities

Solving absolute value inequalities can be a challenging task, but with the right strategies and techniques, it can become more manageable. In this article, we will explore five ways to solve absolute value inequalities, along with examples and explanations to help you understand the concepts better.

Understanding Absolute Value Inequalities

Before we dive into the solutions, let’s first understand what absolute value inequalities are. An absolute value inequality is an inequality that contains an absolute value expression. The absolute value of a number is its distance from zero on the number line, without considering its direction. For example, the absolute value of 5 is 5, and the absolute value of -5 is also 5.

Method 1: Using the Definition of Absolute Value

One way to solve absolute value inequalities is to use the definition of absolute value. According to the definition, |x| ≥ a is equivalent to x ≥ a or x ≤ -a. Similarly, |x| ≤ a is equivalent to -a ≤ x ≤ a.

For example, let’s solve the inequality |x| ≥ 3.

Using the definition of absolute value, we can rewrite the inequality as x ≥ 3 or x ≤ -3.

Method 2: Using the Number Line

Another way to solve absolute value inequalities is to use the number line. To solve an absolute value inequality, we can graph the solutions on a number line.

For example, let’s solve the inequality |x| ≤ 2.

We can graph the solutions on a number line as follows:

The solutions to the inequality are all the numbers between -2 and 2, inclusive.

Method 3: Using the Distance Formula

We can also solve absolute value inequalities using the distance formula. The distance formula states that the distance between two points (x1, y1) and (x2, y2) is given by √((x2 - x1)^2 + (y2 - y1)^2).

For example, let’s solve the inequality |x - 2| ≥ 1.

Using the distance formula, we can rewrite the inequality as √((x - 2)^2) ≥ 1.

Simplifying the inequality, we get x - 2 ≥ 1 or x - 2 ≤ -1.

Solving for x, we get x ≥ 3 or x ≤ 1.

Method 4: Using Algebraic Manipulation

We can also solve absolute value inequalities using algebraic manipulation. To solve an absolute value inequality, we can isolate the absolute value expression and then solve for the variable.

For example, let’s solve the inequality |2x - 3| ≤ 5.

Isolating the absolute value expression, we get |2x - 3| ≤ 5.

Simplifying the inequality, we get -5 ≤ 2x - 3 ≤ 5.

Adding 3 to all sides of the inequality, we get -2 ≤ 2x ≤ 8.

Dividing all sides of the inequality by 2, we get -1 ≤ x ≤ 4.

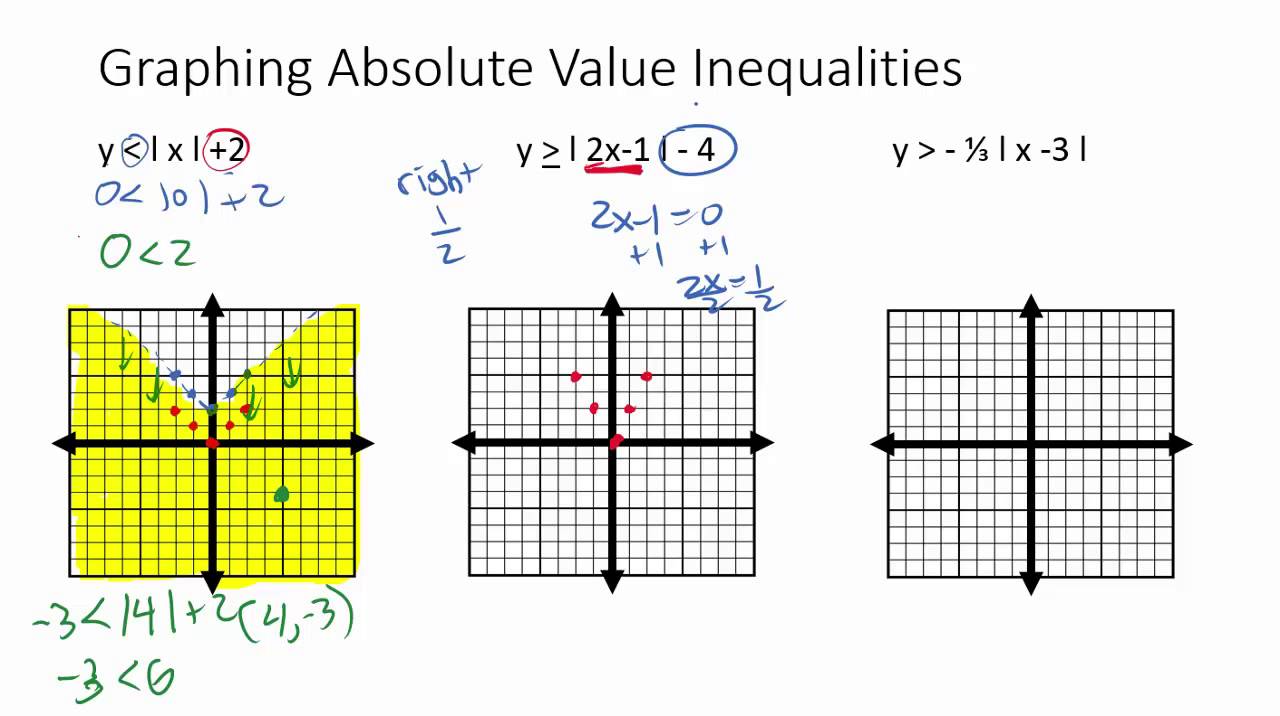
Method 5: Using Graphing

Finally, we can also solve absolute value inequalities using graphing. To solve an absolute value inequality, we can graph the solutions on a coordinate plane.

For example, let’s solve the inequality |x^2 - 4| ≥ 0.

Graphing the solutions on a coordinate plane, we get:

The solutions to the inequality are all the numbers that satisfy the equation x^2 - 4 ≥ 0.

Conclusion

In this article, we explored five ways to solve absolute value inequalities. By using the definition of absolute value, the number line, the distance formula, algebraic manipulation, and graphing, we can solve a wide range of absolute value inequalities. Remember to practice solving different types of absolute value inequalities to become more proficient in solving them.