Domain and Range Graph Worksheet Guide

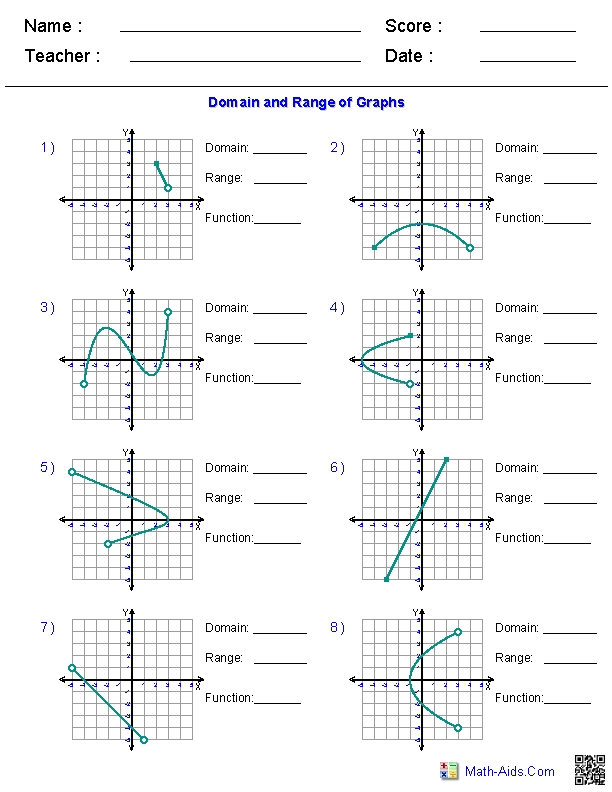
Understanding Domain and Range Graph Worksheet

When working with functions, understanding the domain and range is crucial. The domain of a function is the set of all possible input values (x-values) that the function can accept, while the range is the set of all possible output values (y-values) that the function can produce. In this guide, we will walk you through a step-by-step process of how to complete a domain and range graph worksheet.

Step 1: Review the Function Notation

Before starting the worksheet, make sure you understand the function notation. A function is typically denoted as f(x), where f is the name of the function and x is the input value. For example, f(x) = 2x + 1 is a linear function that takes an input value x and produces an output value f(x).

Step 2: Identify the Type of Function

Identify the type of function represented in the graph. Is it a linear function, quadratic function, or exponential function? Each type of function has its own unique characteristics and rules for determining the domain and range.

Step 3: Determine the Domain

To determine the domain of a function, look for any restrictions on the input values. For example, if the function has a denominator, the denominator cannot be equal to zero. If the function has a square root, the radicand (the value inside the square root) must be non-negative.

• For linear functions, the domain is usually all real numbers unless there are specific restrictions.
• For quadratic functions, the domain is usually all real numbers unless there are specific restrictions.
• For exponential functions, the domain is usually all real numbers.

📝 Note: Pay attention to any holes or gaps in the graph, as these may indicate restrictions on the domain.

Step 4: Determine the Range

To determine the range of a function, look for any restrictions on the output values. For example, if the function has a maximum or minimum value, this will affect the range.

• For linear functions, the range is usually all real numbers unless there are specific restrictions.
• For quadratic functions, the range may be restricted to a specific interval.
• For exponential functions, the range is usually all positive real numbers.

📝 Note: Pay attention to any asymptotes or end behavior, as these may indicate restrictions on the range.

Step 5: Write the Domain and Range in Interval Notation

Once you have determined the domain and range, write them in interval notation. Interval notation uses brackets and parentheses to indicate the inclusion or exclusion of endpoints.

• For example, the domain of a function might be written as (-∞, 3) ∪ (3, ∞), indicating that the function is defined for all values except x = 3.
• The range of a function might be written as [2, ∞), indicating that the function produces all values greater than or equal to 2.

Step 6: Check Your Answers

Finally, check your answers by plugging in test values into the original function. Make sure the values you choose are within the domain and range you determined.

Common Mistakes to Avoid

• Make sure to pay attention to any restrictions on the domain and range.
• Don’t forget to check your answers by plugging in test values.
• Use interval notation correctly to write the domain and range.

Conclusion

Completing a domain and range graph worksheet requires attention to detail and a thorough understanding of function notation and types of functions. By following these steps and avoiding common mistakes, you can become proficient in determining the domain and range of functions.