Convert Fractions with Ease Worksheet
Mastering the Art of Converting Fractions
Converting fractions is a fundamental skill in mathematics that can seem daunting at first, but with practice and the right techniques, it can become second nature. In this worksheet, we will explore the different methods of converting fractions, including converting between mixed numbers and improper fractions, simplifying fractions, and converting fractions to decimals.
Converting Mixed Numbers to Improper Fractions
A mixed number is a combination of a whole number and a fraction. To convert a mixed number to an improper fraction, you need to follow these steps:
- Multiply the whole number by the denominator
- Add the numerator to the product
- Write the result as an improper fraction
For example, let’s convert the mixed number 2 3⁄4 to an improper fraction:
2 x 4 = 8 8 + 3 = 11 11⁄4
So, 2 3⁄4 is equal to 11⁄4.
Converting Improper Fractions to Mixed Numbers
To convert an improper fraction to a mixed number, you need to follow these steps:
- Divide the numerator by the denominator
- Write the result as a whole number and a remainder
- Write the remainder as a fraction
For example, let’s convert the improper fraction 11⁄4 to a mixed number:
11 ÷ 4 = 2 with a remainder of 3 2 3⁄4
So, 11⁄4 is equal to 2 3⁄4.
Simplifying Fractions
Simplifying fractions involves reducing a fraction to its simplest form. To simplify a fraction, you need to find the greatest common divisor (GCD) of the numerator and the denominator, and then divide both numbers by the GCD.
For example, let’s simplify the fraction 6⁄8:
GCD of 6 and 8 is 2 6 ÷ 2 = 3 8 ÷ 2 = 4 3⁄4
So, 6⁄8 is equal to 3⁄4.
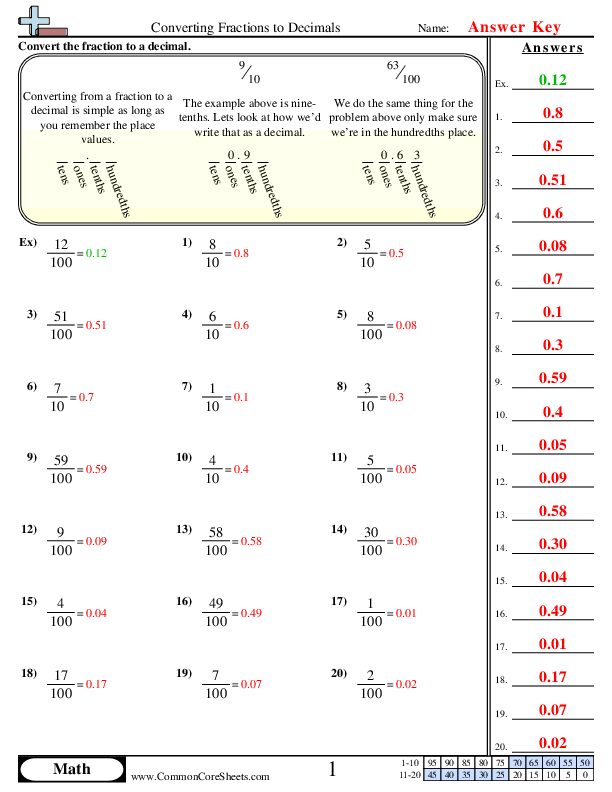
Converting Fractions to Decimals
Converting fractions to decimals involves dividing the numerator by the denominator.
For example, let’s convert the fraction 3⁄4 to a decimal:
3 ÷ 4 = 0.75
So, 3⁄4 is equal to 0.75.
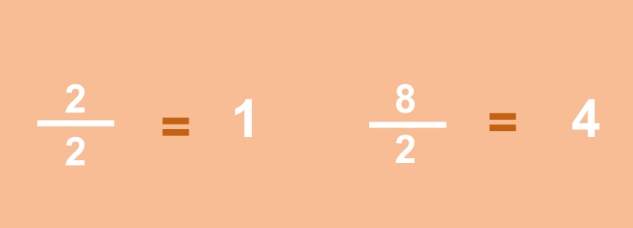
| Fraction | Decimal |
|---|---|
| 1/2 | 0.5 |
| 1/4 | 0.25 |
| 3/4 | 0.75 |
| 2/3 | 0.67 |
📝 Note: When converting fractions to decimals, the result may be a repeating decimal. For example, 1/3 is equal to 0.33, which is a repeating decimal.
Practice Time!
Now it’s time to practice converting fractions. Try converting the following fractions:
- 2 1⁄2 to an improper fraction
- 7⁄2 to a mixed number
- 9⁄12 to a simplified fraction
- 3⁄5 to a decimal
Answers
- 2 1⁄2 = 5⁄2
- 7⁄2 = 3 1⁄2
- 9⁄12 = 3⁄4
- 3⁄5 = 0.6
By mastering the art of converting fractions, you will be able to tackle more complex math problems with ease. Remember to practice regularly and use the techniques outlined in this worksheet to help you become a pro at converting fractions.
In summary, converting fractions involves converting between mixed numbers and improper fractions, simplifying fractions, and converting fractions to decimals. With practice and patience, you can become proficient in converting fractions and take your math skills to the next level.
What is the difference between a mixed number and an improper fraction?
+A mixed number is a combination of a whole number and a fraction, while an improper fraction is a fraction where the numerator is greater than the denominator.
How do you simplify a fraction?
+To simplify a fraction, you need to find the greatest common divisor (GCD) of the numerator and the denominator, and then divide both numbers by the GCD.
What is the purpose of converting fractions to decimals?
+Converting fractions to decimals helps to make calculations easier and more efficient. Decimals are often used in real-world applications, such as finance and science.
Related Terms:
- Multiplying Fractions worksheet pdf
- Fraction Worksheet Grade 5
- Fraction to decimal grade 6
- Fraction to decimal Worksheet
- Subtracting fractions Worksheet