5 Ways to Master Angles of Polygons
Mastering angles of polygons is a fundamental concept in geometry and is crucial for problem-solving in various mathematical and real-world applications. Polygons are two-dimensional shapes with at least three sides, and understanding their angles is essential for calculating perimeter, area, and volume. In this article, we will explore five ways to master angles of polygons.
Understanding the Basics of Angles in Polygons
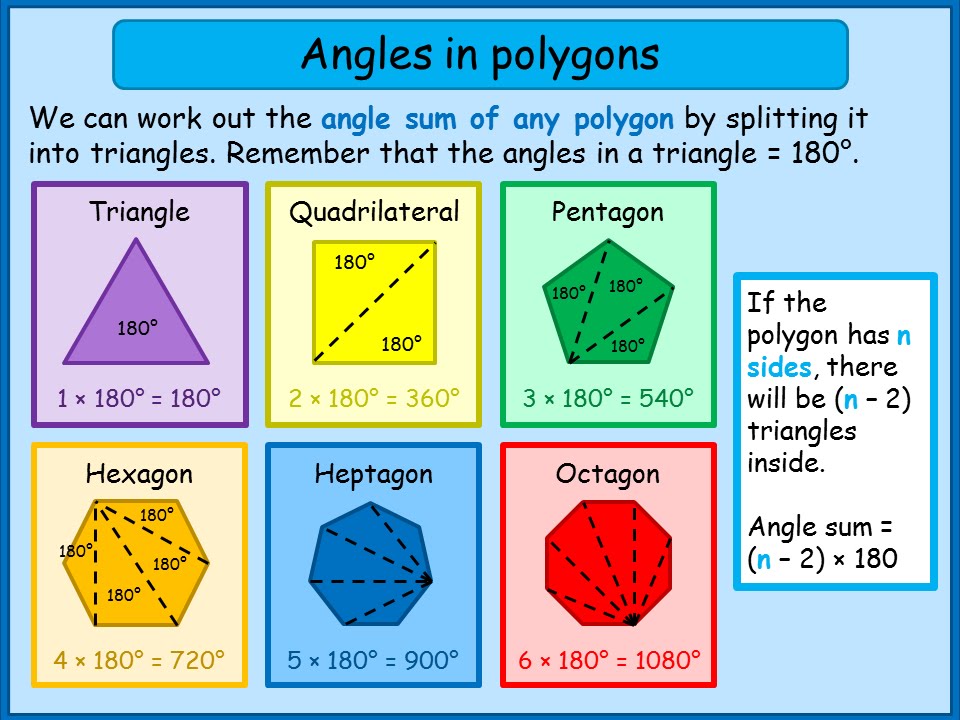
Before we dive into the five ways to master angles of polygons, it’s essential to understand the basics of angles in polygons. In a polygon, an angle is formed by two sides that share a common vertex. The sum of the interior angles of a polygon can be calculated using the formula: (n-2) × 180°, where n is the number of sides of the polygon.
For example, in a triangle (a polygon with three sides), the sum of the interior angles is (3-2) × 180° = 180°. This means that the sum of the interior angles of a triangle is always 180°.
Way 1: Calculating Angles Using the Formula
One way to master angles of polygons is to use the formula (n-2) × 180° to calculate the sum of the interior angles. This formula can be applied to any polygon, regardless of the number of sides.
For example, if we want to calculate the sum of the interior angles of a hexagon (a polygon with six sides), we can use the formula:
(6-2) × 180° = 4 × 180° = 720°
This means that the sum of the interior angles of a hexagon is 720°.
📝 Note: When calculating the sum of interior angles, make sure to subtract 2 from the number of sides to get the correct result.
Way 2: Identifying Types of Angles
Another way to master angles of polygons is to identify the different types of angles that can be formed. In a polygon, there are several types of angles, including:
- Acute angle: An angle that is less than 90°
- Right angle: An angle that is equal to 90°
- Obtuse angle: An angle that is greater than 90° but less than 180°
- Straight angle: An angle that is equal to 180°
- Reflex angle: An angle that is greater than 180° but less than 360°
By identifying the type of angle, you can determine the measure of the angle and calculate the sum of the interior angles of the polygon.
Way 3: Using Properties of Special Polygons
Certain polygons have special properties that can help you master their angles. For example:
- Regular polygons: In a regular polygon, all sides and angles are equal. This means that if you know the measure of one angle, you can calculate the measure of all the other angles.
- Equilateral triangles: An equilateral triangle is a triangle with all sides equal. The measure of each angle in an equilateral triangle is 60°.
- Isosceles triangles: An isosceles triangle is a triangle with two sides equal. The measure of the base angles (the angles opposite the equal sides) is equal.
By understanding the properties of special polygons, you can calculate the measure of their angles and master their geometry.
Way 4: Visualizing Angles Using Diagrams
Visualizing angles using diagrams is another way to master angles of polygons. By drawing a diagram of the polygon, you can see the relationships between the angles and calculate their measures.
For example, if you draw a diagram of a quadrilateral (a polygon with four sides), you can see that the sum of the interior angles is 360°. By identifying the types of angles and using the properties of special polygons, you can calculate the measure of each angle.
Way 5: Practicing with Real-World Applications
Finally, practicing with real-world applications is an excellent way to master angles of polygons. By applying your knowledge of angles to real-world problems, you can reinforce your understanding and develop problem-solving skills.
For example, if you’re designing a building, you need to calculate the angles of the roof to ensure that it is structurally sound. By applying your knowledge of angles, you can calculate the measure of the angles and design a safe and functional building.
| Polygon | Number of Sides | Sum of Interior Angles |
|---|---|---|
| Triangle | 3 | 180° |
| Quadrilateral | 4 | 360° |
| Pentagon | 5 | 540° |
| Hexagon | 6 | 720° |
In conclusion, mastering angles of polygons is a fundamental concept in geometry that requires practice and application. By using the formula (n-2) × 180°, identifying types of angles, using properties of special polygons, visualizing angles using diagrams, and practicing with real-world applications, you can become proficient in calculating and applying angles of polygons.
What is the sum of the interior angles of a triangle?
+The sum of the interior angles of a triangle is 180°.
How do you calculate the sum of the interior angles of a polygon?
+The sum of the interior angles of a polygon can be calculated using the formula (n-2) × 180°, where n is the number of sides of the polygon.
What is the difference between an acute angle and an obtuse angle?
+An acute angle is less than 90°, while an obtuse angle is greater than 90° but less than 180°.