5 Ways to Master Fractions in Equations
Mastering Fractions in Equations: A Comprehensive Guide
Fractions in equations can be a challenging topic for many students. However, with the right approach and practice, anyone can master this concept. In this article, we will explore five effective ways to simplify fractions in equations and improve your problem-solving skills.
1. Understand the Basics of Fractions
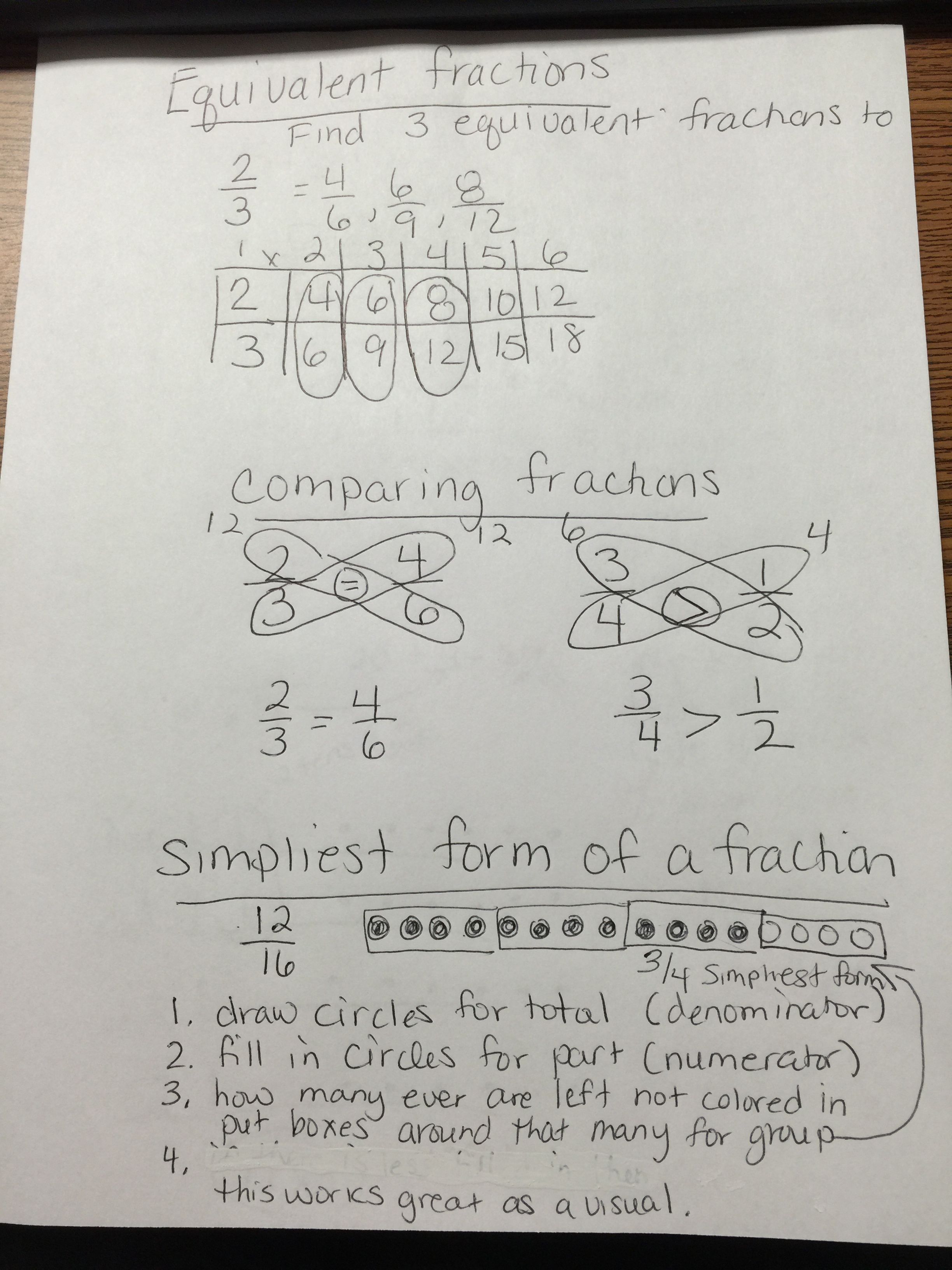
Before diving into fractions in equations, it’s essential to understand the basics of fractions. A fraction represents a part of a whole, and it consists of two parts: the numerator (the top number) and the denominator (the bottom number). To simplify fractions, you need to find the greatest common divisor (GCD) of the numerator and denominator.
📝 Note: The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
For example, to simplify the fraction 6⁄8, you need to find the GCD of 6 and 8, which is 2. Then, divide both numbers by 2 to get the simplified fraction 3⁄4.
2. Learn to Simplify Fractions in Equations
To simplify fractions in equations, you need to follow these steps:
- Identify the fractions in the equation
- Simplify each fraction by finding the GCD of the numerator and denominator
- Rewrite the equation with the simplified fractions
For example, consider the equation:
2⁄4 + 1⁄6 =?
To simplify this equation, follow these steps:
- Identify the fractions: 2⁄4 and 1⁄6
- Simplify each fraction:
- 2⁄4 = 1⁄2 (GCD of 2 and 4 is 2)
- 1⁄6 = 1⁄6 (GCD of 1 and 6 is 1)
- Rewrite the equation: 1⁄2 + 1⁄6 =?
3. Use the Least Common Multiple (LCM) to Add and Subtract Fractions
When adding and subtracting fractions, you need to find the least common multiple (LCM) of the denominators. The LCM is the smallest number that both denominators can divide into evenly.
For example, consider the equation:
1⁄4 + 1⁄6 =?
To add these fractions, follow these steps:
- Find the LCM of 4 and 6, which is 12
- Convert both fractions to have a denominator of 12:
- 1⁄4 = 3⁄12
- 1⁄6 = 2⁄12
- Add the fractions: 3⁄12 + 2⁄12 = 5⁄12
4. Practice with Real-World Examples
To master fractions in equations, it’s essential to practice with real-world examples. Here are a few examples to get you started:
- A recipe calls for 3⁄4 cup of flour. If you want to make half the recipe, how much flour do you need?
- A bookshelf has 5 shelves, and each shelf can hold 3⁄4 of a box of books. If the bookshelf is currently empty, how many boxes of books can you add?
Practicing with real-world examples will help you understand how fractions are used in everyday life and improve your problem-solving skills.
5. Use Online Resources and Games to Make Learning Fun
There are many online resources and games that can make learning fractions fun and engaging. Here are a few examples:
- Khan Academy: Khan Academy has an excellent fraction course that covers the basics of fractions and how to simplify them in equations.
- Math Playground: Math Playground has a variety of fraction games and puzzles that can help you practice your skills in a fun and interactive way.
- Fraction War: Fraction War is a game that allows you to practice comparing fractions and simplifying them in equations.
Using online resources and games can make learning fractions more enjoyable and interactive.
In summary, mastering fractions in equations requires a combination of understanding the basics of fractions, simplifying fractions, using the LCM to add and subtract fractions, practicing with real-world examples, and using online resources and games to make learning fun.
What is the difference between a numerator and a denominator?
+The numerator is the top number in a fraction, and the denominator is the bottom number. The numerator represents the part of the whole, while the denominator represents the total number of parts.
How do I simplify a fraction in an equation?
+To simplify a fraction in an equation, find the greatest common divisor (GCD) of the numerator and denominator. Then, divide both numbers by the GCD to get the simplified fraction.
What is the least common multiple (LCM) of two numbers?
+The least common multiple (LCM) of two numbers is the smallest number that both numbers can divide into evenly. The LCM is used to add and subtract fractions with different denominators.