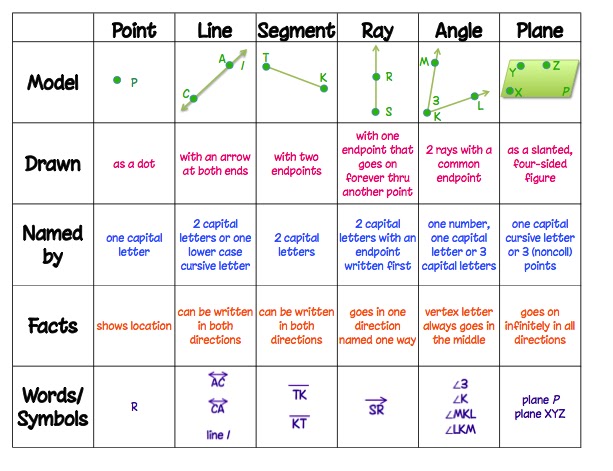
Congruent Triangle Proofs Worksheet

Understanding Congruent Triangle Proofs
Congruent triangle proofs are a fundamental concept in geometry, and they play a crucial role in establishing the relationship between two triangles. When two triangles are congruent, it means that they have the same size and shape. In this blog post, we will delve into the world of congruent triangle proofs and explore the different methods used to prove that two triangles are congruent.
What are Congruent Triangles?
Congruent triangles are triangles that have the same size and shape. This means that their corresponding sides and angles are equal. When two triangles are congruent, we can use the symbol ≅ to denote this relationship. For example, if triangle ABC is congruent to triangle DEF, we can write:
ABC ≅ DEF
Methods of Congruent Triangle Proofs
There are several methods used to prove that two triangles are congruent. These methods include:
- Side-Side-Side (SSS) Postulate: If three sides of one triangle are equal to the corresponding three sides of another triangle, then the two triangles are congruent.
- Side-Angle-Side (SAS) Postulate: If two sides and the included angle of one triangle are equal to the corresponding two sides and included angle of another triangle, then the two triangles are congruent.
- Angle-Side-Angle (ASA) Postulate: If two angles and the included side of one triangle are equal to the corresponding two angles and included side of another triangle, then the two triangles are congruent.
- Angle-Angle-Side (AAS) Postulate: If two angles and a non-included side of one triangle are equal to the corresponding two angles and non-included side of another triangle, then the two triangles are congruent.
SSS Postulate
The SSS postulate states that if three sides of one triangle are equal to the corresponding three sides of another triangle, then the two triangles are congruent. This method is often used when we are given the lengths of the sides of the triangles.
Example: Prove that triangle ABC is congruent to triangle DEF.

| Triangle ABC | Triangle DEF |
|---|---|
| AB = 5 cm | DE = 5 cm |
| BC = 6 cm | EF = 6 cm |
| AC = 7 cm | DF = 7 cm |
Since the corresponding sides of the two triangles are equal, we can conclude that triangle ABC is congruent to triangle DEF.
👉 Note: The SSS postulate is often used when we are given the lengths of the sides of the triangles.
SAS Postulate
The SAS postulate states that if two sides and the included angle of one triangle are equal to the corresponding two sides and included angle of another triangle, then the two triangles are congruent.
Example: Prove that triangle ABC is congruent to triangle DEF.
| Triangle ABC | Triangle DEF |
|---|---|
| AB = 5 cm | DE = 5 cm |
| BC = 6 cm | EF = 6 cm |
| ∠B = 60° | ∠E = 60° |
Since the corresponding sides and included angle of the two triangles are equal, we can conclude that triangle ABC is congruent to triangle DEF.
ASA Postulate
The ASA postulate states that if two angles and the included side of one triangle are equal to the corresponding two angles and included side of another triangle, then the two triangles are congruent.
Example: Prove that triangle ABC is congruent to triangle DEF.
| Triangle ABC | Triangle DEF |
|---|---|
| ∠A = 30° | ∠D = 30° |
| ∠B = 60° | ∠E = 60° |
| AB = 5 cm | DE = 5 cm |
Since the corresponding angles and included side of the two triangles are equal, we can conclude that triangle ABC is congruent to triangle DEF.
AAS Postulate
The AAS postulate states that if two angles and a non-included side of one triangle are equal to the corresponding two angles and non-included side of another triangle, then the two triangles are congruent.
Example: Prove that triangle ABC is congruent to triangle DEF.
| Triangle ABC | Triangle DEF |
|---|---|
| ∠A = 30° | ∠D = 30° |
| ∠B = 60° | ∠E = 60° |
| BC = 6 cm | EF = 6 cm |
Since the corresponding angles and non-included side of the two triangles are equal, we can conclude that triangle ABC is congruent to triangle DEF.
In conclusion, congruent triangle proofs are an essential part of geometry, and they play a vital role in establishing the relationship between two triangles. The different methods used to prove that two triangles are congruent include the SSS, SAS, ASA, and AAS postulates. By understanding these methods, we can determine whether two triangles are congruent or not.
What is the definition of congruent triangles?
+Congruent triangles are triangles that have the same size and shape. This means that their corresponding sides and angles are equal.
What are the different methods used to prove that two triangles are congruent?
+The different methods used to prove that two triangles are congruent include the SSS, SAS, ASA, and AAS postulates.
What is the SSS postulate?
+The SSS postulate states that if three sides of one triangle are equal to the corresponding three sides of another triangle, then the two triangles are congruent.
Related Terms:
- Proving triangles congruent Worksheet pdf
- Proving right triangles congruent Worksheet
- Triangle congruence Proofs Worksheet Kuta