5 Essential Geometry Basics to Master
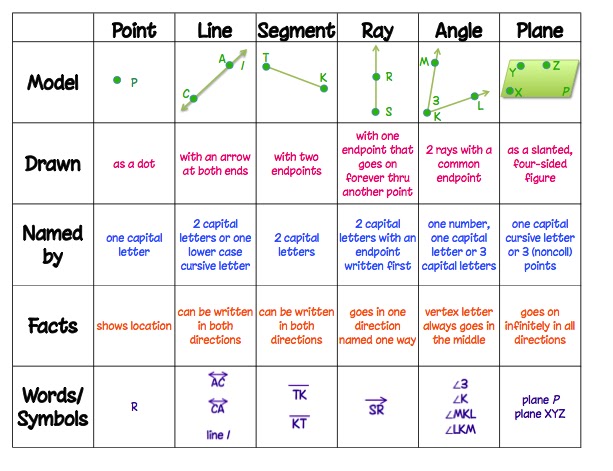
Understanding the Foundations of Geometry
Geometry is a branch of mathematics that deals with the study of shapes, sizes, and positions of objects. It involves understanding the properties and relationships between points, lines, angles, and planes. Mastering the basics of geometry is crucial for problem-solving in various fields, including architecture, engineering, art, and design. In this article, we will explore five essential geometry basics that you should know.
1. Points, Lines, and Planes
The foundation of geometry begins with understanding points, lines, and planes. A point is a location in space, represented by a set of coordinates. A line is a set of points that extend infinitely in two directions, and it can be straight or curved. A plane is a flat surface that extends infinitely in all directions. Understanding these basic concepts is essential for more advanced geometric concepts.
Key Terms:
- Point: A location in space, represented by a set of coordinates.
- Line: A set of points that extend infinitely in two directions.
- Plane: A flat surface that extends infinitely in all directions.
2. Angles and Measurements
Angles are a fundamental part of geometry, and understanding how to measure them is crucial. An angle is formed by two rays sharing a common endpoint, called the vertex. Angles can be classified into different types, including acute, right, obtuse, and straight angles. Measuring angles can be done using a protractor or a compass.
Types of Angles:
- Acute Angle: An angle less than 90 degrees.
- Right Angle: An angle equal to 90 degrees.
- Obtuse Angle: An angle greater than 90 degrees but less than 180 degrees.
- Straight Angle: An angle equal to 180 degrees.
3. Properties of Shapes
Understanding the properties of different shapes is essential in geometry. A shape is a self-contained area with a defined boundary. Common shapes include triangles, quadrilaterals, polygons, and circles. Each shape has its unique properties, such as the number of sides, angles, and symmetry.
Properties of Shapes:
- Triangle: A polygon with three sides and three angles.
- Quadrilateral: A polygon with four sides and four angles.
- Polygon: A shape with at least three sides and angles.
- Circle: A shape with no beginning or end, with all points equidistant from the center.
4. Theorems and Proofs
Geometry involves proving theorems and using logical reasoning to establish the truth of a statement. A theorem is a statement that can be proven true using logical reasoning and evidence. Understanding theorems and proofs is essential for problem-solving in geometry.
Famous Theorems:
- Pythagorean Theorem: a^2 + b^2 = c^2, where a and b are the legs of a right triangle, and c is the hypotenuse.
- Theorem of Thales: The diameter of a circle subtends a right angle at any point on the circle.
5. Geometric Transformations
Geometric transformations involve changing the size, position, or orientation of a shape. Common transformations include translations, rotations, and reflections. Understanding geometric transformations is essential for problem-solving in various fields, including architecture and engineering.
Types of Geometric Transformations:
- Translation: Moving a shape from one position to another without changing its size or orientation.
- Rotation: Turning a shape around a fixed point without changing its size.
- Reflection: Flipping a shape over a line or axis without changing its size.
🔍 Note: Mastering geometric transformations requires understanding the concept of congruent and similar shapes.
In conclusion, mastering the basics of geometry is essential for problem-solving in various fields. Understanding points, lines, and planes, angles and measurements, properties of shapes, theorems and proofs, and geometric transformations will provide a solid foundation for more advanced geometric concepts.
What is the difference between a point and a line?
+A point is a location in space, represented by a set of coordinates, while a line is a set of points that extend infinitely in two directions.
What is the Pythagorean Theorem?
+The Pythagorean Theorem states that a^2 + b^2 = c^2, where a and b are the legs of a right triangle, and c is the hypotenuse.
What is the difference between a translation and a rotation?
+A translation involves moving a shape from one position to another without changing its size or orientation, while a rotation involves turning a shape around a fixed point without changing its size.