4th Grade Fractions Worksheet: Compare with Ease
Understanding Fractions: A Key to Unlocking Math Confidence
For many students, the concept of fractions can be daunting. However, with the right approach, comparing fractions can become second nature. In this article, we will explore the basics of fractions, provide a 4th-grade fractions worksheet, and offer practical tips to help students compare fractions with ease.
What is a Fraction?
A fraction is a way to represent a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many equal parts we have, while the denominator tells us how many parts the whole is divided into.
Example:
Imagine you have a pizza that is divided into 8 slices. You eat 2 of them. The fraction of the pizza you ate is 2⁄8.
Comparing Fractions: The Basics
Comparing fractions involves determining which fraction is larger or smaller. To do this, we need to follow some simple rules:
- If the denominators are the same, the fraction with the larger numerator is larger.
- If the numerators are the same, the fraction with the smaller denominator is larger.
- If both the numerators and denominators are different, we need to find a common denominator to compare the fractions.
Example:
Compare the fractions 1⁄2 and 1⁄4.
- The denominators are different, so we need to find a common denominator. The least common multiple (LCM) of 2 and 4 is 4. We can rewrite the fractions as 2⁄4 and 1⁄4.
- Since the numerators are different, we can see that 2⁄4 is larger than 1⁄4.
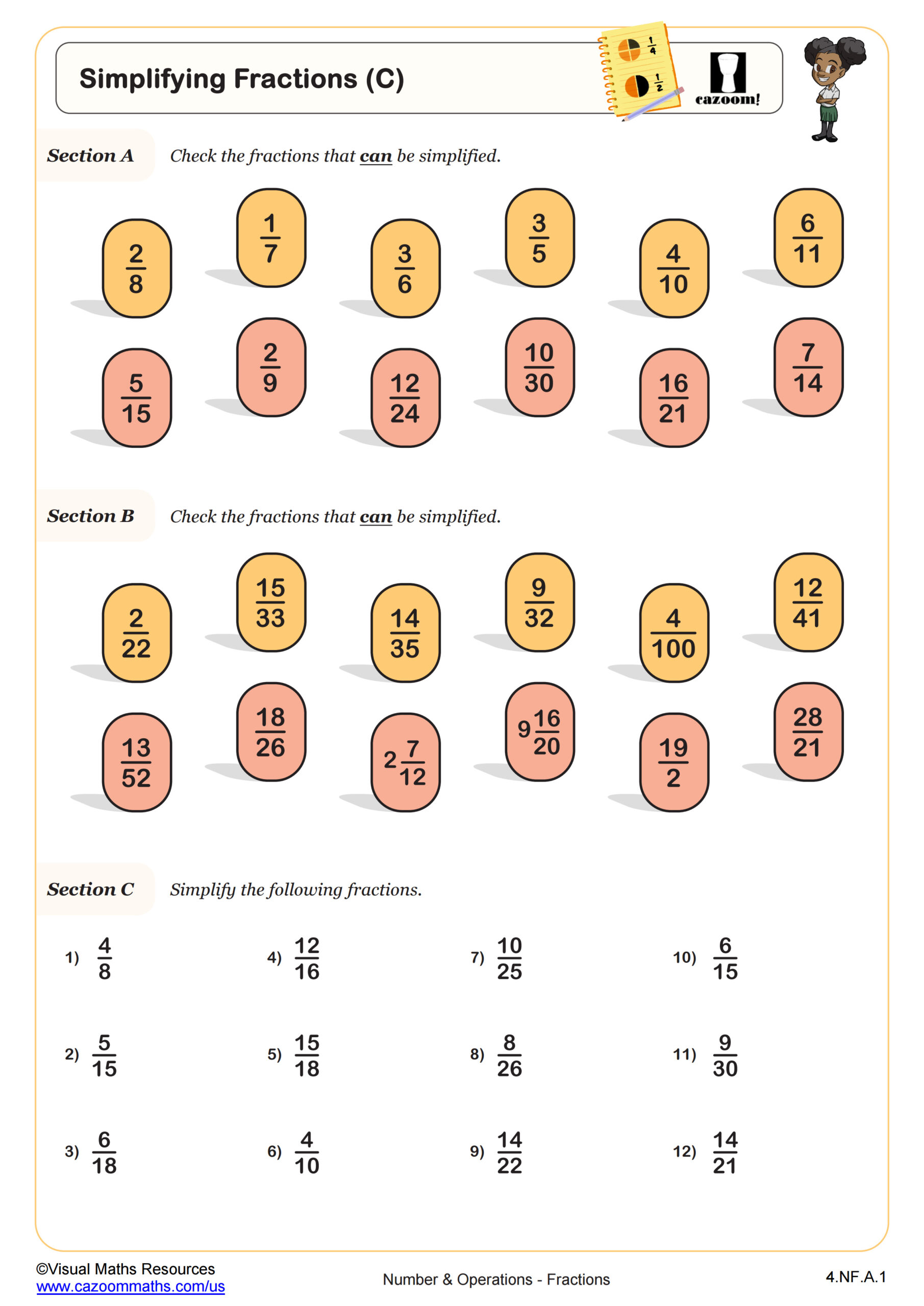
4th Grade Fractions Worksheet
Now it’s time to practice! Here’s a 4th-grade fractions worksheet to help you compare fractions with ease:

| Fraction 1 | Fraction 2 | Compare |
|---|---|---|
| 1/2 | 1/4 | _____ |
| 3/6 | 2/6 | _____ |
| 2/3 | 3/4 | _____ |
| 1/8 | 1/6 | _____ |
| 3/4 | 2/3 | _____ |
Tips for Comparing Fractions
- Always check if the denominators are the same before comparing fractions.
- If the denominators are different, find a common denominator to compare the fractions.
- Use visual aids such as fraction strips or circles to help you compare fractions.
- Practice, practice, practice! The more you practice comparing fractions, the more confident you’ll become.
💡 Note: Remember to always simplify fractions before comparing them. Simplifying fractions means dividing both the numerator and denominator by the greatest common divisor (GCD).
Real-World Applications of Fractions
Fractions are not just limited to math problems. They have real-world applications in cooking, science, and finance. For example:
- Cooking: When following a recipe, you may need to measure out ingredients using fractions.
- Science: Fractions are used to represent ratios of different substances in a mixture.
- Finance: Fractions are used to calculate interest rates and investment returns.
By mastering fractions, you’ll be able to tackle a wide range of real-world problems with confidence.
What is the difference between a numerator and a denominator?
+The numerator is the top number in a fraction that tells us how many equal parts we have. The denominator is the bottom number that tells us how many parts the whole is divided into.
How do I simplify a fraction?
+To simplify a fraction, divide both the numerator and denominator by the greatest common divisor (GCD).
Can I compare fractions with different denominators?
+Yes, you can compare fractions with different denominators by finding a common denominator.
By the end of this article, you should have a solid understanding of fractions and how to compare them with ease. Remember to practice regularly and use visual aids to help you better understand the concepts. With time and practice, you’ll become a master of fractions and be able to tackle even the toughest math problems with confidence.