Central and Inscribed Angles Math Problems Made Easy
Understanding Central and Inscribed Angles in Circles
Circles are an essential part of geometry, and angles within circles can often be confusing for students to grasp. Two crucial concepts in circle geometry are central angles and inscribed angles. In this post, we’ll break down these concepts, explain how they’re related, and provide examples and exercises to help solidify your understanding.
What is a Central Angle?
A central angle is an angle formed by two radii (or rays) that intersect at the center of a circle. The vertex of the angle is at the center of the circle, and the sides of the angle are radii. The central angle is also known as a central arc angle.
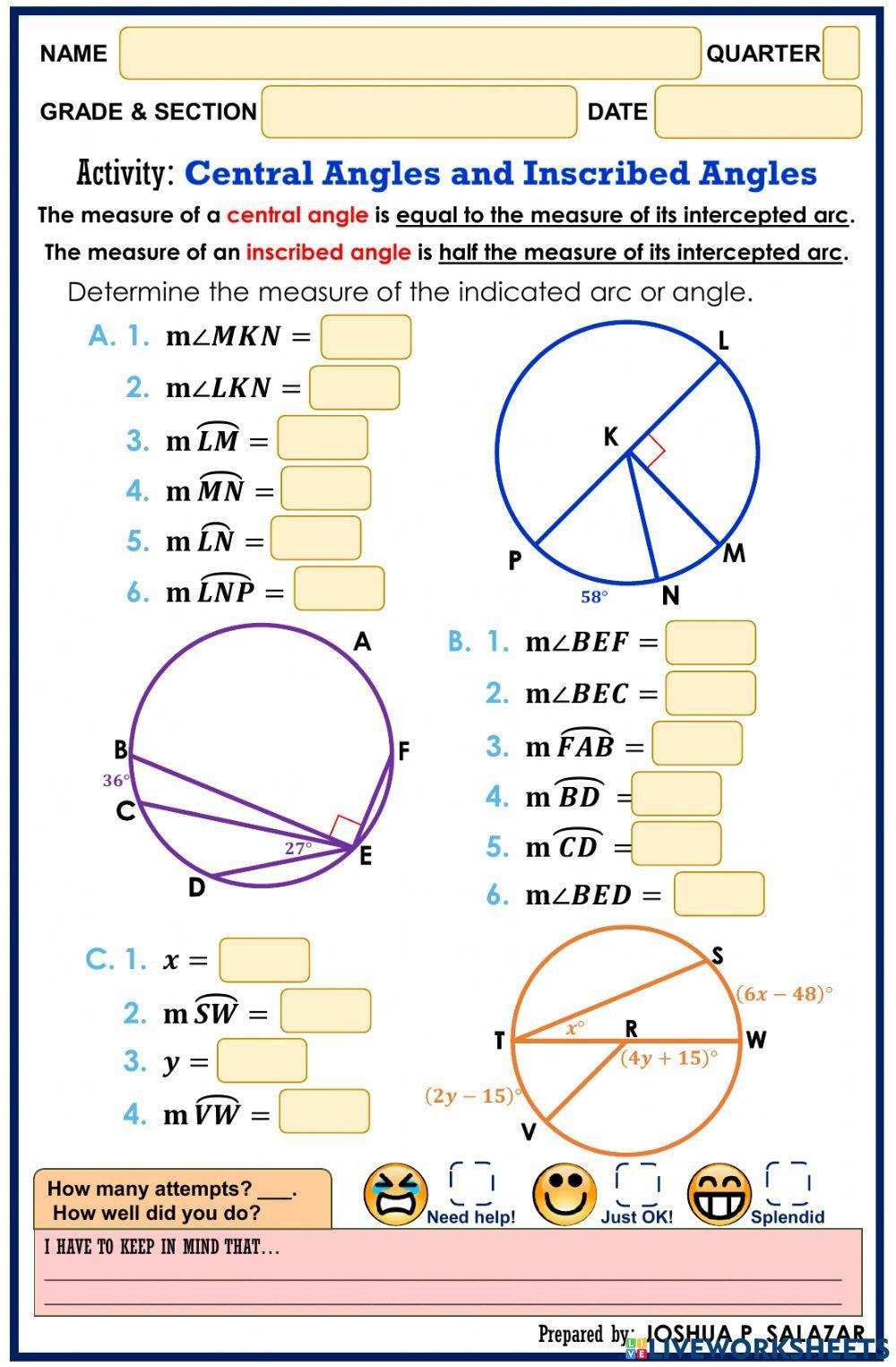
The measure of a central angle is equal to the measure of its intercepted arc. This means that if you know the measure of the central angle, you can find the measure of the intercepted arc, and vice versa.
What is an Inscribed Angle?
An inscribed angle is an angle formed by two chords (or secants) that intersect on the circle. The vertex of the angle is on the circle, and the sides of the angle are chords. Inscribed angles are also known as inscribed arc angles.
The measure of an inscribed angle is equal to half the measure of its intercepted arc. This means that if you know the measure of the inscribed angle, you can find the measure of the intercepted arc, and vice versa.
Key Differences Between Central and Inscribed Angles
| Characteristics | Central Angle | Inscribed Angle |
|---|---|---|
| Vertex | At the center of the circle | On the circle |
| Sides | Radii | Chords |
| Measure | Equal to the measure of its intercepted arc | Half the measure of its intercepted arc |
Relationship Between Central and Inscribed Angles
The central angle and inscribed angle are related in that they both intercept the same arc. The measure of the central angle is twice the measure of the inscribed angle.
Let’s consider an example:
Suppose we have a circle with a central angle of 60° and an inscribed angle that intercepts the same arc. What is the measure of the inscribed angle?
Since the central angle is 60°, the inscribed angle is half of that, or 30°.
📝 Note: This relationship holds true only when the central angle and inscribed angle intercept the same arc.
Examples and Exercises
Here are a few examples to help solidify your understanding:
Example 1
Find the measure of the central angle that intercepts an arc of 80°.
Solution
Since the central angle is equal to the measure of its intercepted arc, the central angle measures 80°.
Example 2
Find the measure of the inscribed angle that intercepts an arc of 120°.
Solution
Since the inscribed angle is half the measure of its intercepted arc, the inscribed angle measures 60°.
Exercise 1
Find the measure of the central angle that intercepts an arc of 50°.
Exercise 2
Find the measure of the inscribed angle that intercepts an arc of 90°.
Conclusion
Central angles and inscribed angles are two fundamental concepts in circle geometry. Understanding the relationship between these angles and their intercepted arcs is crucial for solving problems in geometry. By practicing with examples and exercises, you’ll become more comfortable working with central and inscribed angles and be better equipped to tackle more complex geometry problems.
What is the difference between a central angle and an inscribed angle?
+A central angle is formed by two radii that intersect at the center of a circle, while an inscribed angle is formed by two chords that intersect on the circle.
What is the relationship between a central angle and an inscribed angle?
+The central angle is equal to the measure of its intercepted arc, while the inscribed angle is half the measure of its intercepted arc.
How do I find the measure of a central angle?
+The measure of a central angle is equal to the measure of its intercepted arc.
Related Terms:
- Inscribed Angles Worksheet PDF
- Central and Inscribed angles practice
- Central Angles Worksheet
- Central and inscribed angles quiz