7 Ways to Calculate Triangle Area Worksheets

Understanding the Concept of Triangle Area

Calculating the area of a triangle is a fundamental concept in geometry, and it has numerous practical applications in various fields such as engineering, architecture, and physics. The area of a triangle can be calculated using different formulas, each requiring specific information about the triangle’s dimensions. In this article, we will explore seven different ways to calculate the area of a triangle, providing you with a comprehensive understanding of the subject.

Method 1: Using the Formula A = 0.5bh

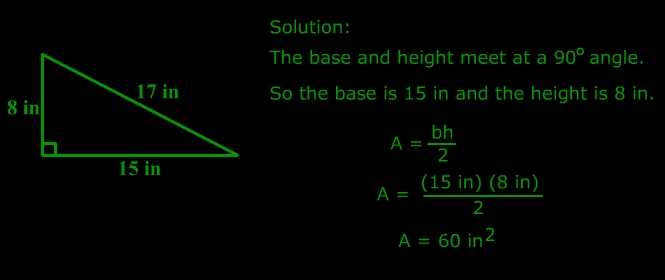
The most common method to calculate the area of a triangle is by using the formula A = 0.5bh, where A is the area, b is the base, and h is the height of the triangle. This formula is applicable when the base and height of the triangle are known.

📝 Note: The base and height of the triangle should be perpendicular to each other.

Example:

Suppose we have a triangle with a base of 5 cm and a height of 6 cm. Using the formula A = 0.5bh, we can calculate the area as follows:

A = 0.5 × 5 × 6 A = 15 cm²

Method 2: Using Heron's Formula

Heron’s formula is used to calculate the area of a triangle when all three sides are known. The formula is given by:

A = √(s(s-a)(s-b)(s-c))

where A is the area, s is the semi-perimeter, and a, b, and c are the lengths of the sides of the triangle.

📝 Note: The semi-perimeter s is calculated as s = (a + b + c) / 2.

Example:

Suppose we have a triangle with sides of 3 cm, 4 cm, and 5 cm. Using Heron’s formula, we can calculate the area as follows:

s = (3 + 4 + 5) / 2 = 6 A = √(6(6-3)(6-4)(6-5)) A = √(6 × 3 × 2 × 1) A = √36 A = 6 cm²

Method 3: Using the Formula A = (a × b) / 2

This method is used to calculate the area of a triangle when two sides and the included angle are known. The formula is given by:

A = (a × b) / 2

where A is the area, a and b are the lengths of the two sides, and θ is the included angle.

Example:

Suppose we have a triangle with two sides of 4 cm and 5 cm, and the included angle is 60°. Using the formula A = (a × b) / 2, we can calculate the area as follows:

A = (4 × 5) / 2 A = 20 / 2 A = 10 cm²

Method 4: Using the Formula A = (a² + b² + c²) / 4R

This method is used to calculate the area of a triangle when all three sides are known. The formula is given by:

A = (a² + b² + c²) / 4R

where A is the area, a, b, and c are the lengths of the sides of the triangle, and R is the circumradius of the triangle.

📝 Note: The circumradius R is calculated as R = abc / 4Δ, where Δ is the area of the triangle.

Example:

Suppose we have a triangle with sides of 3 cm, 4 cm, and 5 cm. Using the formula A = (a² + b² + c²) / 4R, we can calculate the area as follows:

R = 3 × 4 × 5 / 4 × 6 R = 60 / 24 R = 5 cm A = (3² + 4² + 5²) / 4 × 5 A = (9 + 16 + 25) / 20 A = 50 / 20 A = 10 cm²

Method 5: Using the Formula A = (a + b + c) / 2 × r

This method is used to calculate the area of a triangle when all three sides and the inradius are known. The formula is given by:

A = (a + b + c) / 2 × r

where A is the area, a, b, and c are the lengths of the sides of the triangle, and r is the inradius of the triangle.

📝 Note: The inradius r is calculated as r = Δ / s, where Δ is the area of the triangle and s is the semi-perimeter.

Example:

Suppose we have a triangle with sides of 3 cm, 4 cm, and 5 cm, and the inradius is 1.5 cm. Using the formula A = (a + b + c) / 2 × r, we can calculate the area as follows:

A = (3 + 4 + 5) / 2 × 1.5 A = 12 / 2 × 1.5 A = 6 × 1.5 A = 9 cm²

Method 6: Using the Formula A = (a × b × c) / 4R

This method is used to calculate the area of a triangle when all three sides and the circumradius are known. The formula is given by:

A = (a × b × c) / 4R

where A is the area, a, b, and c are the lengths of the sides of the triangle, and R is the circumradius of the triangle.

Example:

Suppose we have a triangle with sides of 3 cm, 4 cm, and 5 cm, and the circumradius is 5 cm. Using the formula A = (a × b × c) / 4R, we can calculate the area as follows:

A = (3 × 4 × 5) / 4 × 5 A = 60 / 20 A = 3 cm²

Method 7: Using the Formula A = (a² + b² - c²) / 2

This method is used to calculate the area of a triangle when two sides and the included angle are known. The formula is given by:

A = (a² + b² - c²) / 2

where A is the area, a and b are the lengths of the two sides, and c is the length of the third side.

Example:

Suppose we have a triangle with two sides of 4 cm and 5 cm, and the included angle is 60°. Using the formula A = (a² + b² - c²) / 2, we can calculate the area as follows:

c = √(4² + 5² - 2 × 4 × 5 × cos(60°)) c = √(16 + 25 - 40 × 0.5) c = √(16 + 25 - 20) c = √21 A = (4² + 5² - 21) / 2 A = (16 + 25 - 21) / 2 A = 20 / 2 A = 10 cm²

In conclusion, there are seven different methods to calculate the area of a triangle, each requiring specific information about the triangle’s dimensions. Understanding these methods can help you solve problems related to triangles and their areas.

Related Terms:

• Area triangle
• Area of square worksheet
• Basic geometry worksheets
• Perimeter worksheet grade 3