Angles in Polygons Worksheet for Math Mastery
Mastering Angles in Polygons: A Comprehensive Guide
Angles in polygons are a fundamental concept in geometry, and understanding them is crucial for math mastery. In this article, we will delve into the world of polygons, exploring the different types of angles, their properties, and how to calculate them.
What is a Polygon?
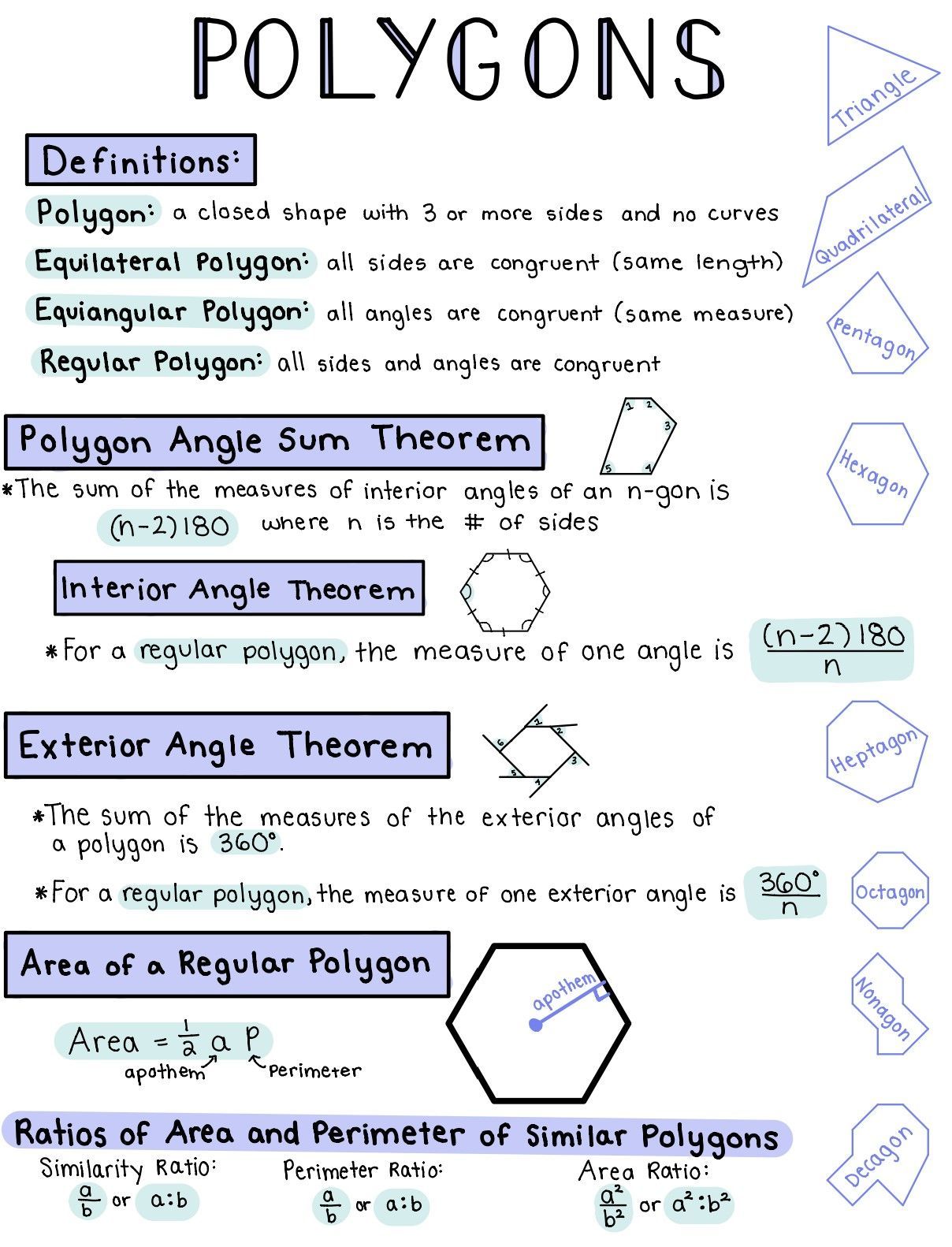
A polygon is a two-dimensional shape with at least three sides. The sides of a polygon are line segments that connect to form a closed shape. Polygons can be classified into different types based on the number of sides they have. The most common types of polygons include triangles, quadrilaterals, pentagons, and hexagons.
Types of Angles in Polygons
There are several types of angles in polygons, including:
- Interior Angles: These are the angles formed inside the polygon by two adjacent sides.
- Exterior Angles: These are the angles formed outside the polygon by two adjacent sides.
- Vertex Angles: These are the angles formed at a vertex (corner) of the polygon.
Properties of Angles in Polygons
Angles in polygons have several important properties, including:
- Sum of Interior Angles: The sum of the interior angles of a polygon is always equal to (n-2) x 180 degrees, where n is the number of sides.
- Sum of Exterior Angles: The sum of the exterior angles of a polygon is always equal to 360 degrees.
- Interior Angle Theorem: The interior angle theorem states that the sum of the interior angles of a triangle is always 180 degrees.
Calculating Angles in Polygons
Calculating angles in polygons can be a challenging task, but with the right formulas and techniques, it can be made easier. Here are some common formulas and techniques used to calculate angles in polygons:
- Interior Angle Formula: The interior angle formula is used to calculate the measure of each interior angle in a polygon. The formula is: Interior Angle = (n-2) x 180 / n
- Exterior Angle Formula: The exterior angle formula is used to calculate the measure of each exterior angle in a polygon. The formula is: Exterior Angle = 360 / n
- Triangle Angle Sum Theorem: The triangle angle sum theorem states that the sum of the interior angles of a triangle is always 180 degrees.
📝 Note: When calculating angles in polygons, it's essential to ensure that the polygon is a convex polygon, meaning that all the interior angles are less than 180 degrees.
Worksheet: Angles in Polygons
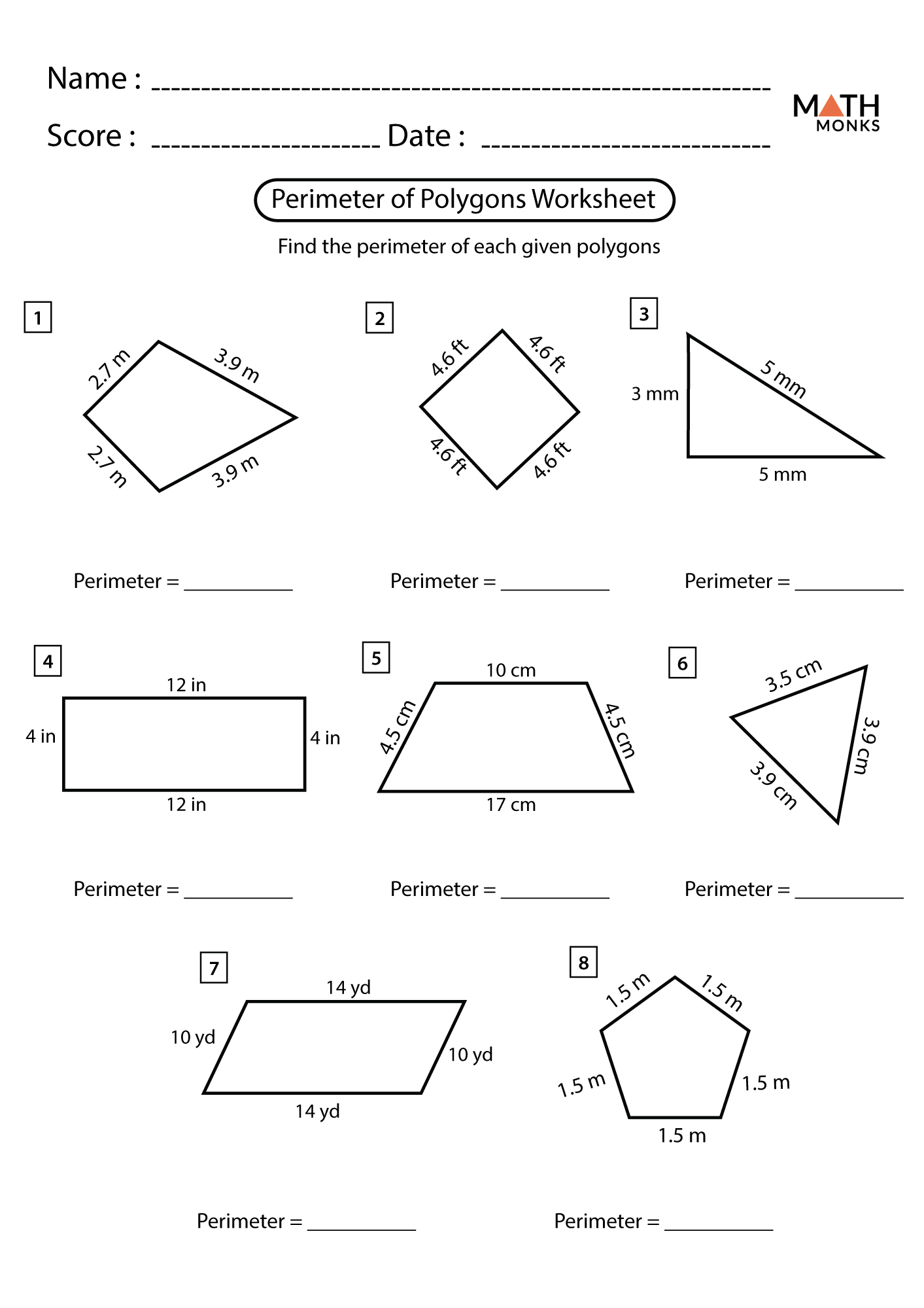
Now that we have covered the basics of angles in polygons, it’s time to put your knowledge to the test. Here is a worksheet with 10 questions to help you practice calculating angles in polygons:
| Question | Polygon | Number of Sides | Angle Type | Answer |
|---|---|---|---|---|
| 1 | Triangle | 3 | Interior Angle | 60 degrees |
| 2 | Quadrilateral | 4 | Exterior Angle | 90 degrees |
| 3 | Pentagon | 5 | Interior Angle | 108 degrees |
| 4 | Hexagon | 6 | Exterior Angle | 60 degrees |
| 5 | Heptagon | 7 | Interior Angle | 128.57 degrees |
| 6 | Octagon | 8 | Exterior Angle | 45 degrees |
| 7 | Nonagon | 9 | Interior Angle | 140 degrees |
| 8 | Decagon | 10 | Exterior Angle | 36 degrees |
| 9 | Dodecagon | 12 | Interior Angle | 150 degrees |
| 10 | Icosagon | 20 | Exterior Angle | 18 degrees |
Answers and Solutions
Here are the answers and solutions to the worksheet:
| Question | Answer | Solution |
|---|---|---|
| 1 | 60 degrees | Interior Angle = (3-2) x 180 / 3 = 60 degrees |
| 2 | 90 degrees | Exterior Angle = 360 / 4 = 90 degrees |
| 3 | 108 degrees | Interior Angle = (5-2) x 180 / 5 = 108 degrees |
| 4 | 60 degrees | Exterior Angle = 360 / 6 = 60 degrees |
| 5 | 128.57 degrees | Interior Angle = (7-2) x 180 / 7 = 128.57 degrees |
| 6 | 45 degrees | Exterior Angle = 360 / 8 = 45 degrees |
| 7 | 140 degrees | Interior Angle = (9-2) x 180 / 9 = 140 degrees |
| 8 | 36 degrees | Exterior Angle = 360 / 10 = 36 degrees |
| 9 | 150 degrees | Interior Angle = (12-2) x 180 / 12 = 150 degrees |
| 10 | 18 degrees | Exterior Angle = 360 / 20 = 18 degrees |
Now that we have completed the worksheet, let’s summarize the key points:
- Angles in polygons are a fundamental concept in geometry.
- There are several types of angles in polygons, including interior angles, exterior angles, and vertex angles.
- The sum of the interior angles of a polygon is always equal to (n-2) x 180 degrees, where n is the number of sides.
- The sum of the exterior angles of a polygon is always equal to 360 degrees.
- Calculating angles in polygons can be done using formulas and techniques, such as the interior angle formula and the exterior angle formula.
Let’s move on to the FAQ section to answer some common questions about angles in polygons.
What is the sum of the interior angles of a polygon?
+The sum of the interior angles of a polygon is always equal to (n-2) x 180 degrees, where n is the number of sides.
What is the sum of the exterior angles of a polygon?
+The sum of the exterior angles of a polygon is always equal to 360 degrees.
How do you calculate the interior angle of a polygon?
+The interior angle of a polygon can be calculated using the formula: Interior Angle = (n-2) x 180 / n, where n is the number of sides.