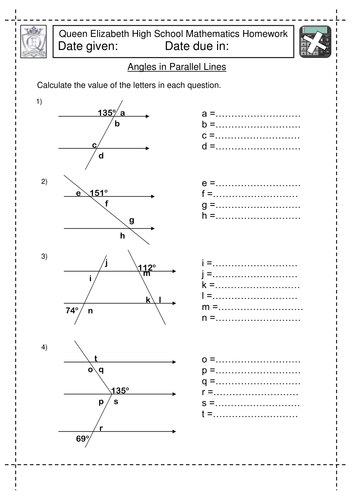
Angles in Parallel Lines Worksheet for Easy Learning

Understanding Angles in Parallel Lines
Angles in parallel lines is a fundamental concept in geometry that helps students understand the relationships between angles formed when a transversal intersects two or more parallel lines. In this worksheet, we will explore the different types of angles formed in parallel lines and provide examples and exercises to help students master this concept.
What are Parallel Lines?
Parallel lines are two or more lines that lie in the same plane and never intersect, no matter how far they are extended. In other words, parallel lines have the same slope and are always the same distance apart.
Types of Angles in Parallel Lines
When a transversal intersects two parallel lines, it forms several types of angles, including:
- Corresponding angles: These are angles that are in the same position on each line, but on opposite sides of the transversal.
- Alternate interior angles: These are angles that are on the inside of the parallel lines, but on opposite sides of the transversal.
- Alternate exterior angles: These are angles that are on the outside of the parallel lines, but on opposite sides of the transversal.
- Interior angles on the same side of the transversal: These are angles that are on the same side of the transversal, but on opposite sides of the parallel lines.
Properties of Angles in Parallel Lines
Here are some important properties of angles in parallel lines:
- Corresponding angles are equal: This means that if two lines are parallel, the corresponding angles formed by a transversal are always equal.
- Alternate interior angles are equal: This means that if two lines are parallel, the alternate interior angles formed by a transversal are always equal.
- Alternate exterior angles are equal: This means that if two lines are parallel, the alternate exterior angles formed by a transversal are always equal.
- Interior angles on the same side of the transversal are supplementary: This means that if two lines are parallel, the interior angles on the same side of the transversal add up to 180 degrees.
Examples and Exercises
Here are some examples and exercises to help you practice working with angles in parallel lines:
Example 1:
In the diagram below, line AB is parallel to line CD. Find the measure of angle E.

Since line AB is parallel to line CD, we know that corresponding angles are equal. Therefore, angle E is equal to angle F.
Exercise 1:
In the diagram below, line AB is parallel to line CD. Find the measure of angle G.

Example 2:
In the diagram below, line AB is parallel to line CD. Find the measure of angle H.

Since line AB is parallel to line CD, we know that alternate interior angles are equal. Therefore, angle H is equal to angle J.
Exercise 2:
In the diagram below, line AB is parallel to line CD. Find the measure of angle K.

Table of Angle Relationships
Here is a table summarizing the angle relationships in parallel lines:
| Angle Type | Relationship |
|---|---|
| Corresponding angles | Equal |
| Alternate interior angles | Equal |
| Alternate exterior angles | Equal |
| Interior angles on the same side of the transversal | Supplementary |
📝 Note: Remember to always check the diagram carefully and identify the types of angles before applying the angle relationships.
In conclusion, angles in parallel lines is a fundamental concept in geometry that helps students understand the relationships between angles formed when a transversal intersects two or more parallel lines. By mastering this concept, students can solve a wide range of problems involving angles and parallel lines.
What are parallel lines?
+Parallel lines are two or more lines that lie in the same plane and never intersect, no matter how far they are extended.
What are corresponding angles?
+Corresponding angles are angles that are in the same position on each line, but on opposite sides of the transversal.
What is the relationship between alternate interior angles?
+Alternate interior angles are equal.