Angles in a Triangle Worksheet Exercises
Angles in a Triangle Worksheet Exercises
Triangles are one of the most fundamental concepts in geometry, and understanding angles in a triangle is crucial for various mathematical and real-world applications. In this worksheet, we will explore various exercises to help you master the concept of angles in a triangle.
Types of Angles in a Triangle
Before we dive into the exercises, let’s review the different types of angles in a triangle:
- Acute Angle: An angle whose measure is less than 90 degrees.
- Right Angle: An angle whose measure is exactly 90 degrees.
- Obtuse Angle: An angle whose measure is greater than 90 degrees but less than 180 degrees.
- Straight Angle: An angle whose measure is exactly 180 degrees.
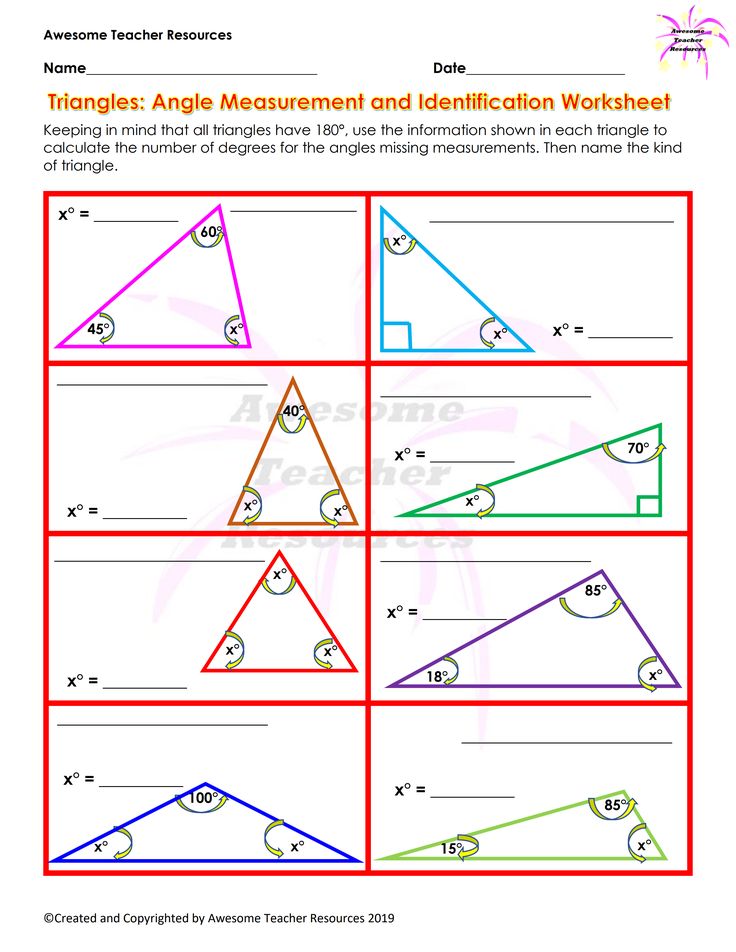
Exercise 1: Finding the Third Angle in a Triangle
In a triangle, the sum of the interior angles is always 180 degrees. Use this fact to find the third angle in the following triangles:
- Triangle ABC: ∠A = 60°, ∠B = 80°, ∠C =?
- Triangle DEF: ∠D = 45°, ∠E = 90°, ∠F =?
- Triangle GHI: ∠G = 120°, ∠H = 30°, ∠I =?
💡 Note: Use the fact that the sum of the interior angles in a triangle is 180 degrees to find the third angle.
Exercise 2: Identifying Types of Angles in a Triangle
Identify the type of angle in each of the following triangles:
| Triangle | Angle | Type of Angle |
|---|---|---|
| ABC | ∠A = 75° | |
| DEF | ∠D = 120° | |
| GHI | ∠G = 90° |
📝 Note: Use the definitions of acute, right, obtuse, and straight angles to identify the type of angle in each triangle.
Exercise 3: Solving Angle Problems in a Triangle
Solve the following problems involving angles in a triangle:
- In triangle ABC, ∠A = 2x° and ∠B = 3x°. If ∠C = 90°, find the value of x.
- In triangle DEF, ∠D = x° and ∠E = 2x°. If ∠F = 120°, find the value of x.
🤔 Note: Use algebraic techniques to solve for the unknown variable x.
Exercise 4: Finding the Measure of an Exterior Angle in a Triangle
The measure of an exterior angle in a triangle is equal to the sum of the remote interior angles. Find the measure of the exterior angle in each of the following triangles:
- Triangle ABC: ∠A = 60°, ∠B = 80°
- Triangle DEF: ∠D = 45°, ∠E = 90°
🌐 Note: Use the fact that the measure of an exterior angle is equal to the sum of the remote interior angles.
As we conclude this worksheet, remember that understanding angles in a triangle is essential for various mathematical and real-world applications. By mastering these concepts, you will be well-equipped to tackle more complex problems in geometry and beyond.
What is the sum of the interior angles in a triangle?
+
The sum of the interior angles in a triangle is always 180 degrees.
What is the difference between an acute angle and an obtuse angle?
+
An acute angle is an angle whose measure is less than 90 degrees, while an obtuse angle is an angle whose measure is greater than 90 degrees but less than 180 degrees.
How do you find the measure of an exterior angle in a triangle?
+
The measure of an exterior angle in a triangle is equal to the sum of the remote interior angles.