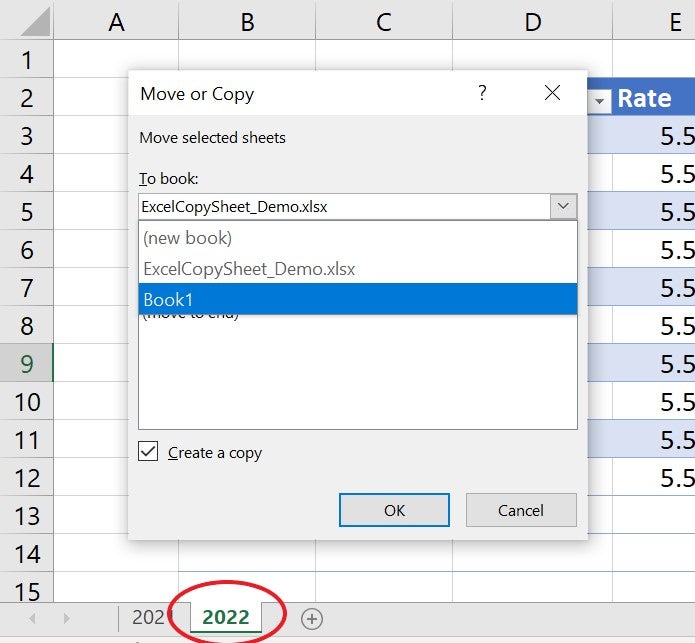
Angle Relationships in Circles Worksheet Solutions

Understanding Angle Relationships in Circles
Angles and circles are fundamental concepts in geometry, and understanding their relationships is crucial for solving various mathematical problems. This worksheet will guide you through the solutions to angle relationships in circles, providing a comprehensive understanding of the subject.
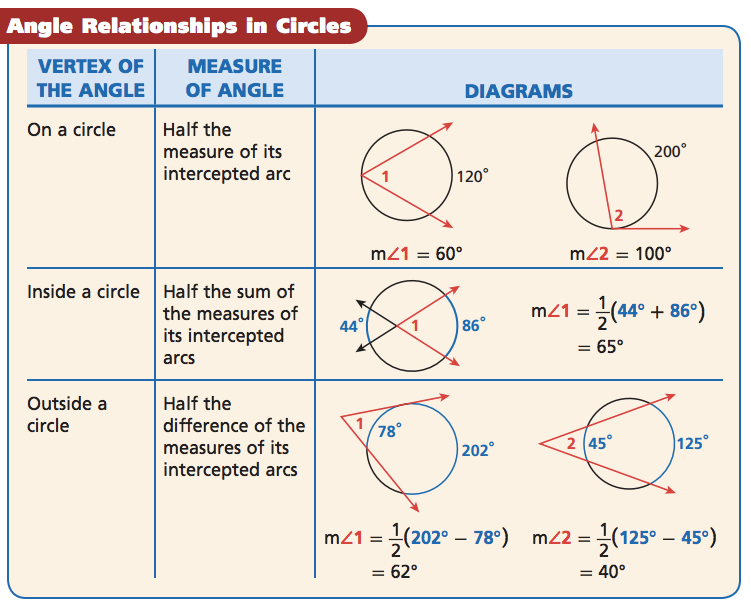
Central Angles
A central angle is an angle whose vertex is at the center of a circle. The measure of a central angle is equal to the measure of its intercepted arc.
Example 1: Find the measure of the central angle ∠AOB in the given circle.
| Measure of arc AB | 120° |
Solution: Since the measure of a central angle is equal to the measure of its intercepted arc, we can write:
m∠AOB = m(arc AB) = 120°
📝 Note: The measure of a central angle is always equal to the measure of its intercepted arc.
Insight Angles
An inscribed angle is an angle whose vertex is on a circle. The measure of an inscribed angle is equal to half the measure of its intercepted arc.
Example 2: Find the measure of the inscribed angle ∠XYZ in the given circle.
| Measure of arc XY | 100° |
Solution: Since the measure of an inscribed angle is equal to half the measure of its intercepted arc, we can write:
m∠XYZ = (1⁄2)m(arc XY) = (1⁄2)(100°) = 50°
📝 Note: The measure of an inscribed angle is always half the measure of its intercepted arc.
Angles Formed by Secants and Tangents
Secants and tangents are lines that intersect a circle at two or one points, respectively. The angle formed by two secants or two tangents is equal to half the difference of the measures of the intercepted arcs.
Example 3: Find the measure of the angle ∠PQR formed by two secants in the given circle.
| Measure of arc PQ | 60° |
| Measure of arc QR | 120° |
Solution: Since the angle formed by two secants is equal to half the difference of the measures of the intercepted arcs, we can write:
m∠PQR = (1⁄2)(m(arc QR) - m(arc PQ)) = (1⁄2)(120° - 60°) = (1⁄2)(60°) = 30°
📝 Note: The angle formed by two secants or two tangents is equal to half the difference of the measures of the intercepted arcs.
Angles Formed by Secants and Tangents (External Angle)
The angle formed by a secant and a tangent is equal to half the measure of the intercepted arc.
Example 4: Find the measure of the angle ∠MNO formed by a secant and a tangent in the given circle.
| Measure of arc MN | 80° |
Solution: Since the angle formed by a secant and a tangent is equal to half the measure of the intercepted arc, we can write:
m∠MNO = (1⁄2)m(arc MN) = (1⁄2)(80°) = 40°
📝 Note: The angle formed by a secant and a tangent is equal to half the measure of the intercepted arc.
In conclusion, understanding angle relationships in circles is crucial for solving various mathematical problems. By mastering the concepts of central angles, inscribed angles, and angles formed by secants and tangents, you can confidently tackle complex problems and develop a deeper understanding of geometry.
What is the measure of a central angle?
+The measure of a central angle is equal to the measure of its intercepted arc.
What is the measure of an inscribed angle?
+The measure of an inscribed angle is equal to half the measure of its intercepted arc.
What is the angle formed by two secants?
+The angle formed by two secants is equal to half the difference of the measures of the intercepted arcs.
Related Terms:
- Angle relationships In circle s calculator