Mastering Angle Pair Relationships Made Easy
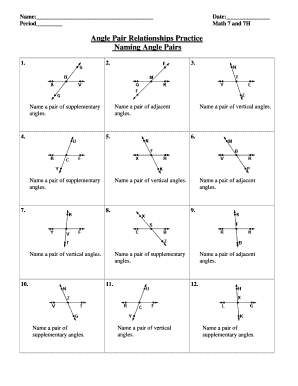
Understanding Angle Pair Relationships
Angle pair relationships are a fundamental concept in geometry, and mastering them is essential for solving various problems in mathematics and real-world applications. In this blog post, we will delve into the world of angle pair relationships, exploring their types, properties, and applications.
What are Angle Pairs?
An angle pair is a set of two angles that share a common vertex and a common side. The angles can be either adjacent (next to each other) or non-adjacent (not next to each other). Angle pairs can be classified into different types based on their relationship with each other.
Types of Angle Pairs
There are several types of angle pairs, including:
- Complementary Angles: Two angles whose measures add up to 90 degrees.
- Supplementary Angles: Two angles whose measures add up to 180 degrees.
- Adjacent Angles: Two angles that share a common vertex and a common side.
- Vertical Angles: Two angles that are opposite each other and share a common vertex.
- Linear Pair Angles: Two angles that form a straight line and share a common vertex.
Properties of Angle Pairs
Each type of angle pair has its unique properties, which are essential for solving problems. Here are some of the key properties:
- Complementary Angles: The sum of the measures of two complementary angles is always 90 degrees.
- Supplementary Angles: The sum of the measures of two supplementary angles is always 180 degrees.
- Adjacent Angles: The sum of the measures of two adjacent angles is always 180 degrees.
- Vertical Angles: Vertical angles are always congruent (equal in measure).
- Linear Pair Angles: The sum of the measures of two linear pair angles is always 180 degrees.
Applications of Angle Pair Relationships
Angle pair relationships have numerous applications in various fields, including:
- Architecture: Understanding angle pair relationships is crucial for designing buildings, bridges, and other structures.
- Engineering: Angle pair relationships are used to design and optimize systems, such as gears, levers, and pulleys.
- Physics: Angle pair relationships are essential for understanding motion, forces, and energy.
- Computer Science: Angle pair relationships are used in computer graphics, game development, and robotics.
Real-World Examples
Here are some real-world examples of angle pair relationships:
- Building Design: When designing a building, architects use angle pair relationships to ensure that the walls, floors, and roofs are properly aligned.
- Gears and Levers: In mechanical systems, angle pair relationships are used to optimize the performance of gears and levers.
- Computer Graphics: Angle pair relationships are used to create 3D models and animations in computer graphics.
🔍 Note: Understanding angle pair relationships is essential for solving problems in mathematics and real-world applications.
Conclusion
Mastering angle pair relationships is a fundamental skill that can help you solve various problems in mathematics and real-world applications. By understanding the different types of angle pairs, their properties, and applications, you can develop a deeper understanding of geometry and its practical uses.
What is the difference between complementary and supplementary angles?
+Complementary angles are two angles whose measures add up to 90 degrees, while supplementary angles are two angles whose measures add up to 180 degrees.
What is the property of vertical angles?
+Vertical angles are always congruent (equal in measure).
How are angle pair relationships used in real-world applications?
+Angle pair relationships are used in various fields, including architecture, engineering, physics, and computer science, to design and optimize systems, models, and structures.