5 Essential Functions to Master in Algebra 1

Unlocking the Fundamentals of Algebra 1
Algebra 1 is a crucial branch of mathematics that provides a foundation for more advanced math subjects, such as geometry, trigonometry, and calculus. Mastering the essential functions in Algebra 1 is vital for students to succeed in their mathematical journey. In this article, we will explore the five essential functions to master in Algebra 1, along with practical examples and tips to help you become proficient.
1. Solving Linear Equations
Linear equations are a fundamental concept in Algebra 1. A linear equation is an equation in which the highest power of the variable (usually x) is 1. The general form of a linear equation is:
ax + b = c
where a, b, and c are constants.
To solve linear equations, you need to isolate the variable x. This can be done by adding, subtracting, multiplying, or dividing both sides of the equation by the same value.
Example: Solve the equation 2x + 5 = 11
🤔 Note: To solve this equation, we need to isolate x. We can do this by subtracting 5 from both sides of the equation.
2x + 5 - 5 = 11 - 5 2x = 6 x = 6 ÷ 2 x = 3
2. Graphing Linear Equations
Graphing linear equations is an essential skill in Algebra 1. A linear equation can be graphed on a coordinate plane, which consists of x and y axes. The x-axis represents the input values, while the y-axis represents the output values.
To graph a linear equation, you need to find the x and y intercepts. The x-intercept is the point where the line crosses the x-axis, while the y-intercept is the point where the line crosses the y-axis.
Example: Graph the equation y = 2x + 3
| x | y |
|---|---|
| -2 | -1 |
| -1 | 1 |
| 0 | 3 |
| 1 | 5 |
| 2 | 7 |
3. Solving Quadratic Equations
Quadratic equations are another crucial concept in Algebra 1. A quadratic equation is an equation in which the highest power of the variable (usually x) is 2. The general form of a quadratic equation is:
ax^2 + bx + c = 0
where a, b, and c are constants.
To solve quadratic equations, you can use factoring, the quadratic formula, or graphing.
Example: Solve the equation x^2 + 4x + 4 = 0
🤔 Note: To solve this equation, we can use factoring. The equation can be factored as (x + 2)(x + 2) = 0.
x + 2 = 0 x = -2
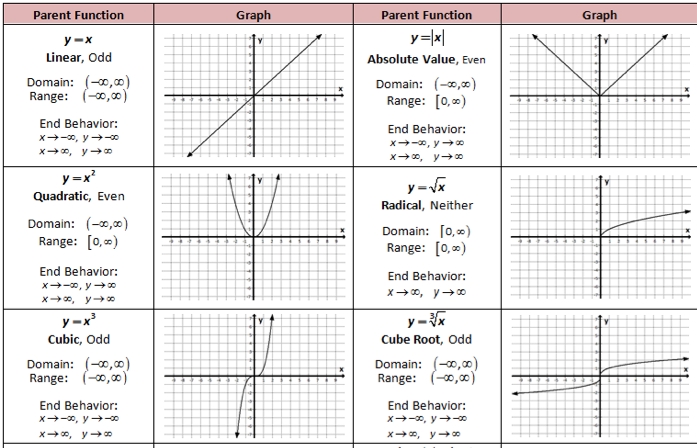
4. Working with Functions
Functions are a fundamental concept in Algebra 1. A function is a relation between a set of inputs (called the domain) and a set of possible outputs (called the range).
To work with functions, you need to understand the concept of domain and range. The domain is the set of all possible input values, while the range is the set of all possible output values.
Example: Find the domain and range of the function f(x) = 2x + 1
Domain: All real numbers Range: All real numbers
5. Analyzing Systems of Equations
Systems of equations are a critical concept in Algebra 1. A system of equations is a set of two or more equations that are solved simultaneously.
To analyze systems of equations, you need to understand the concept of substitution and elimination. Substitution involves solving one equation for a variable and then substituting that value into the other equation. Elimination involves adding or subtracting the equations to eliminate one variable.
Example: Solve the system of equations:
2x + 3y = 7 x - 2y = -3
🤔 Note: To solve this system, we can use substitution. We can solve the second equation for x and then substitute that value into the first equation.
x = -3 + 2y 2(-3 + 2y) + 3y = 7 -6 + 4y + 3y = 7 7y = 13 y = 13 ÷ 7 y = 1.86
To summarize, mastering the essential functions in Algebra 1 requires a deep understanding of linear equations, graphing, quadratic equations, functions, and systems of equations. With practice and patience, you can become proficient in these areas and develop a strong foundation for more advanced math subjects.
As you continue to explore the world of Algebra 1, remember to:
- Practice regularly to reinforce your understanding
- Break down complex problems into simpler steps
- Use visual aids, such as graphs and tables, to help you understand the concepts
- Seek help from teachers, tutors, or online resources when needed
By following these tips and mastering the essential functions in Algebra 1, you will be well on your way to success in mathematics.
What is the difference between a linear equation and a quadratic equation?
+A linear equation is an equation in which the highest power of the variable (usually x) is 1, while a quadratic equation is an equation in which the highest power of the variable (usually x) is 2.
How do I graph a linear equation?
+To graph a linear equation, you need to find the x and y intercepts. The x-intercept is the point where the line crosses the x-axis, while the y-intercept is the point where the line crosses the y-axis.
What is the quadratic formula?
+The quadratic formula is a formula that can be used to solve quadratic equations. The formula is x = (-b ± √(b^2 - 4ac)) / 2a, where a, b, and c are the coefficients of the quadratic equation.
Related Terms:
- Algebra Functions Worksheet with answers
- Functions Algebra 1 pdf
- Functions Worksheet with answers pdf
- Graphing Functions Worksheet Algebra 2



