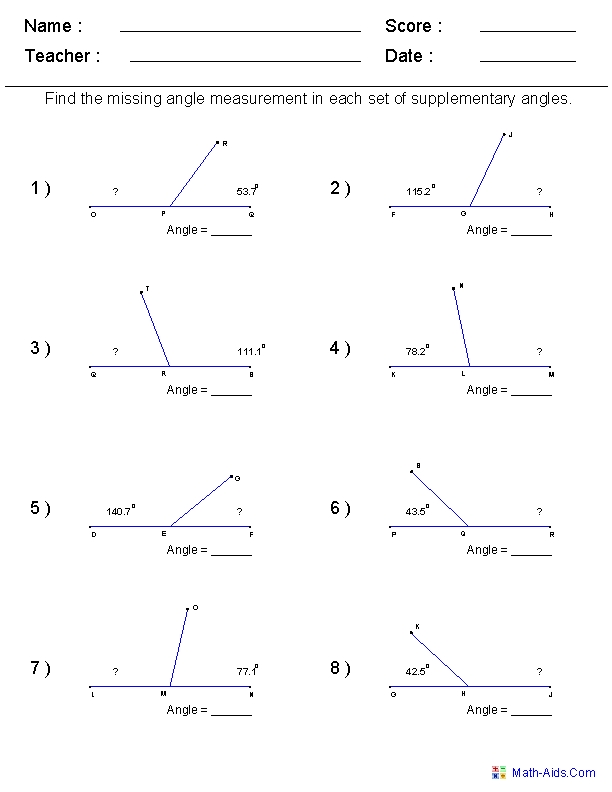
Similar Triangles Proof Worksheet Answer Key

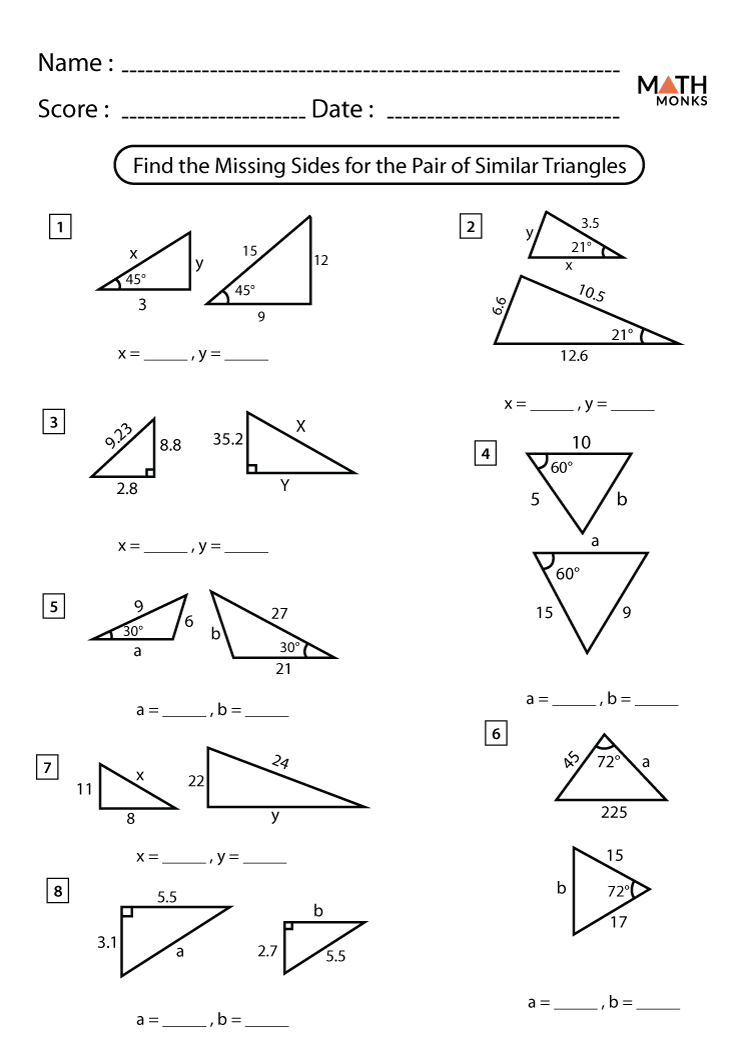
Understanding Similar Triangles

Similar triangles are a fundamental concept in geometry, and they play a crucial role in various mathematical and real-world applications. In this article, we will delve into the world of similar triangles, exploring their definition, properties, and applications. We will also provide a proof worksheet answer key to help you better understand the concepts.

What are Similar Triangles?

Similar triangles are triangles that have the same shape, but not necessarily the same size. This means that their corresponding angles are equal, and their corresponding sides are proportional. In other words, if two triangles are similar, their angles are congruent, and their sides are in proportion.

Properties of Similar Triangles

Similar triangles have several key properties that make them useful in various mathematical and real-world applications. Some of the most important properties of similar triangles include:

• Angle-Angle (AA) Similarity: If two triangles have two pairs of congruent angles, then the triangles are similar.
• Side-Side-Side (SSS) Similarity: If two triangles have three pairs of congruent sides, then the triangles are similar.
• Side-Angle-Side (SAS) Similarity: If two triangles have two pairs of congruent sides and the included angle is congruent, then the triangles are similar.

Proof of Similar Triangles

Now that we have explored the definition and properties of similar triangles, let’s move on to the proof. The proof of similar triangles involves showing that the corresponding angles and sides of two triangles are congruent and proportional, respectively.

Proof Worksheet

Here is a proof worksheet on similar triangles:

Section 1: Angle-Angle (AA) Similarity

1. Given: ∆ABC and ∆DEF, with ∠A ≅ ∠D and ∠B ≅ ∠E Prove: ∆ABC ∼ ∆DEF

Solution

1. ∠A ≅ ∠D (given)
2. ∠B ≅ ∠E (given)
3. ∠C ≅ ∠F (corresponding angles are congruent)
4. ∆ABC ∼ ∆DEF (AA similarity)

Section 2: Side-Side-Side (SSS) Similarity

1. Given: ∆GHI and ∆JKL, with GH ≅ JK, HI ≅ KL, and GI ≅ JL Prove: ∆GHI ∼ ∆JKL

Solution

1. GH ≅ JK (given)
2. HI ≅ KL (given)
3. GI ≅ JL (given)
4. ∆GHI ∼ ∆JKL (SSS similarity)

Section 3: Side-Angle-Side (SAS) Similarity

1. Given: ∆MNO and ∆PQR, with MN ≅ PQ, ∠M ≅ ∠P, and NO ≅ QR Prove: ∆MNO ∼ ∆PQR

Solution

1. MN ≅ PQ (given)
2. ∠M ≅ ∠P (given)
3. NO ≅ QR (given)
4. ∆MNO ∼ ∆PQR (SAS similarity)

Answer Key

Here is the answer key for the proof worksheet:

1. ∆ABC ∼ ∆DEF
2. ∆GHI ∼ ∆JKL
3. ∆MNO ∼ ∆PQR

Notes

• 📝 Note: The proof of similar triangles involves showing that the corresponding angles and sides of two triangles are congruent and proportional, respectively.

• 📝 Note: The AA, SSS, and SAS similarity theorems can be used to prove that two triangles are similar.

Conclusion

In conclusion, similar triangles are a fundamental concept in geometry, and they play a crucial role in various mathematical and real-world applications. The proof of similar triangles involves showing that the corresponding angles and sides of two triangles are congruent and proportional, respectively. By understanding the properties and proof of similar triangles, you can better appreciate their importance in mathematics and real-world applications.

FAQ Section