Solving 1 Step Equations Made Easy
Understanding the Basics of 1 Step Equations
One step equations are simple algebraic equations that can be solved in just one step. These equations typically involve a single variable, such as x or y, and a constant term. The goal is to isolate the variable by performing a single operation, such as addition, subtraction, multiplication, or division. One step equations are a fundamental concept in algebra and are often used as a building block for more complex equations.
Types of 1 Step Equations
There are four main types of one step equations, each involving a different operation:
- Addition Equations: These equations involve adding a constant term to the variable. For example: x + 3 = 5
- Subtraction Equations: These equations involve subtracting a constant term from the variable. For example: x - 2 = 7
- Multiplication Equations: These equations involve multiplying the variable by a constant term. For example: 4x = 20
- Division Equations: These equations involve dividing the variable by a constant term. For example: x ÷ 2 = 9
Solving 1 Step Equations
Solving one step equations is a straightforward process that involves performing the opposite operation to isolate the variable. Here are some examples:
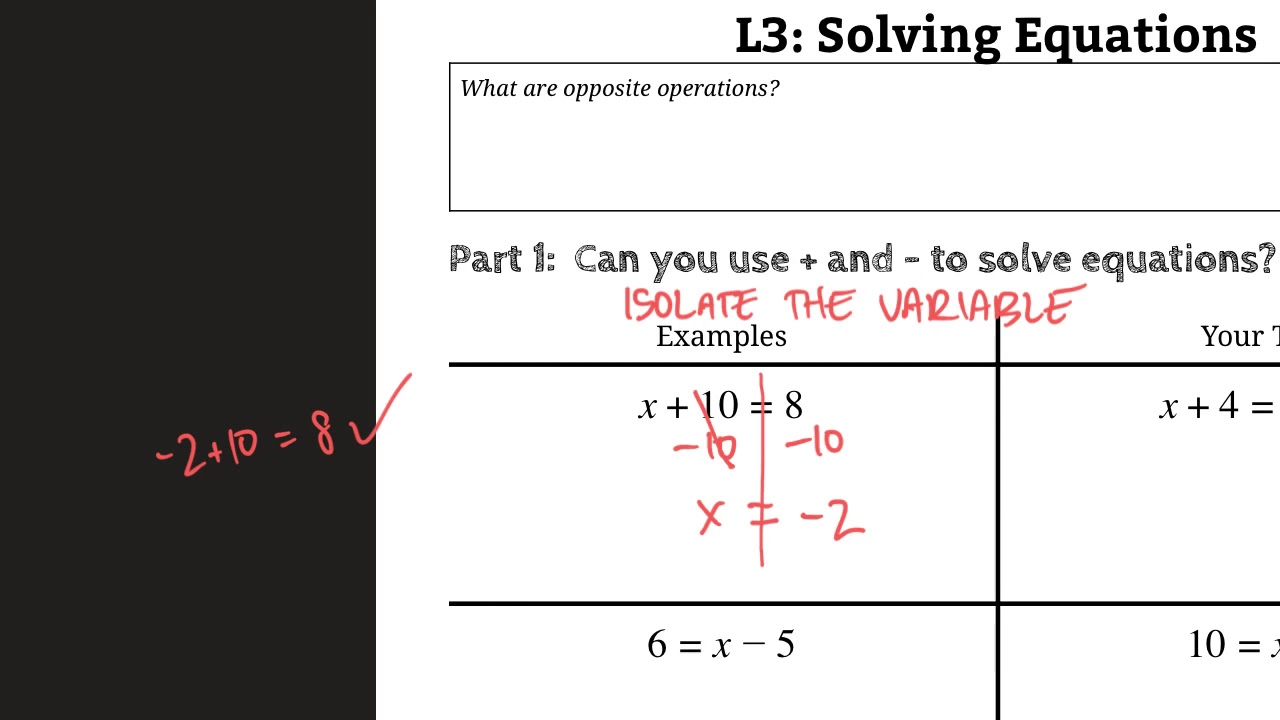
- Addition Equations: To solve for x, subtract the constant term from both sides of the equation. For example: x + 3 = 5 → x = 5 - 3 → x = 2
- Subtraction Equations: To solve for x, add the constant term to both sides of the equation. For example: x - 2 = 7 → x = 7 + 2 → x = 9
- Multiplication Equations: To solve for x, divide both sides of the equation by the constant term. For example: 4x = 20 → x = 20 ÷ 4 → x = 5
- Division Equations: To solve for x, multiply both sides of the equation by the constant term. For example: x ÷ 2 = 9 → x = 9 × 2 → x = 18
📝 Note: When solving one step equations, it's essential to perform the same operation on both sides of the equation to maintain equality.
Examples and Practice
Here are some examples of one step equations with solutions:

| Equation | Solution |
|---|---|
| x + 2 = 9 | x = 9 - 2 → x = 7 |
| x - 4 = 3 | x = 3 + 4 → x = 7 |
| 3x = 24 | x = 24 ÷ 3 → x = 8 |
| x ÷ 3 = 6 | x = 6 × 3 → x = 18 |
Try solving these one step equations on your own:
- x + 1 = 8
- x - 5 = 2
- 2x = 16
- x ÷ 4 = 9
Tips and Tricks
Here are some tips and tricks for solving one step equations:
- Read the equation carefully: Make sure you understand the operation involved and the variable you’re solving for.
- Perform the opposite operation: To isolate the variable, perform the opposite operation on both sides of the equation.
- Check your solution: Plug your solution back into the original equation to ensure it’s true.
Real-World Applications
One step equations have many real-world applications, such as:
- Science: One step equations are used to solve problems involving measurement, such as converting between units.
- Finance: One step equations are used to calculate interest rates, investments, and other financial transactions.
- Cooking: One step equations are used to scale recipes up or down.
What is a one step equation?
+A one step equation is a simple algebraic equation that can be solved in just one step.
How do I solve a one step equation?
+To solve a one step equation, perform the opposite operation to isolate the variable.
What are some real-world applications of one step equations?
+One step equations have many real-world applications, including science, finance, and cooking.
In summary, solving one step equations is a straightforward process that involves performing the opposite operation to isolate the variable. By understanding the different types of one step equations and practicing solving them, you’ll become proficient in no time. Remember to read the equation carefully, perform the opposite operation, and check your solution to ensure accuracy.