5 Ways to Master Volume of Irregular Shapes
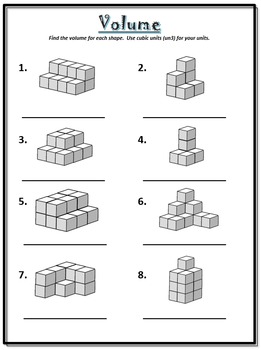
Understanding the Concept of Volume
The concept of volume is a fundamental idea in mathematics and physics, representing the amount of three-dimensional space occupied by an object or shape. While calculating the volume of regular shapes like cubes, spheres, and cylinders can be straightforward, determining the volume of irregular shapes can be more challenging. In this article, we will explore five methods to help you master the calculation of volumes of irregular shapes.
Method 1: Decomposition into Simpler Shapes
One effective way to calculate the volume of an irregular shape is to break it down into simpler, more manageable shapes. This method involves identifying the individual components of the irregular shape and calculating their volumes separately. For example, consider an irregular shape composed of a rectangular prism and a triangular prism.
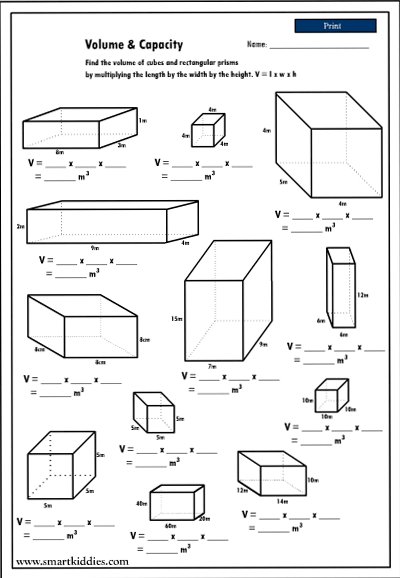
| Shape | Volume Formula | Volume Calculation |
|---|---|---|
| Rectangular Prism | V = lwh | V = 5 × 3 × 2 = 30 cubic units |
| Triangular Prism | V = (1/2) × base × height × length | V = (1/2) × 4 × 6 × 3 = 36 cubic units |
By adding the volumes of the individual shapes, we can determine the total volume of the irregular shape.
📝 Note: This method is particularly useful when dealing with complex shapes that can be broken down into simpler components.
Method 2: Using the Dissection Method
The dissection method involves dividing an irregular shape into smaller, more manageable pieces, and then reassembling them to form a simpler shape whose volume can be easily calculated. This method requires careful planning and execution to ensure accurate results.
For instance, consider an irregular shape that can be dissected into a set of smaller triangular prisms.

By reassembling the smaller triangular prisms, we can form a simpler shape, such as a rectangular prism, whose volume can be easily calculated.
📝 Note: The dissection method can be time-consuming and requires careful planning to ensure accurate results.
Method 3: Using Cavalieri's Principle
Cavalieri’s Principle states that if two shapes have equal altitudes and corresponding cross-sectional areas, then their volumes are equal. This principle can be applied to calculate the volume of an irregular shape by comparing it to a simpler shape with known volume.
For example, consider an irregular shape with a base area of 20 square units and a height of 5 units. By comparing it to a rectangular prism with the same base area and height, we can determine the volume of the irregular shape.
| Shape | Volume Formula | Volume Calculation |
|---|---|---|
| Rectangular Prism | V = lwh | V = 20 × 5 = 100 cubic units |
By applying Cavalieri’s Principle, we can conclude that the volume of the irregular shape is also 100 cubic units.
📝 Note: Cavalieri's Principle is particularly useful when dealing with shapes that have equal altitudes and corresponding cross-sectional areas.
Method 4: Using the Method of Indivisibles
The method of indivisibles involves dividing an irregular shape into an infinite number of infinitesimally small pieces, and then summing up their volumes to determine the total volume of the shape. This method is often used in calculus to calculate the volumes of complex shapes.
For example, consider an irregular shape that can be divided into an infinite number of infinitesimally small rectangular prisms.

By summing up the volumes of the individual rectangular prisms, we can determine the total volume of the irregular shape.
📝 Note: The method of indivisibles requires a strong understanding of calculus and is often used in advanced mathematical applications.
Method 5: Using 3D Printing and Scanning Technology
In recent years, 3D printing and scanning technology have become increasingly popular in various fields, including mathematics and engineering. These technologies can be used to calculate the volume of an irregular shape by creating a physical model of the shape and then scanning it to determine its volume.
For example, consider an irregular shape that can be 3D printed and then scanned using a 3D scanner.

By using specialized software, we can determine the volume of the irregular shape with high accuracy.
📝 Note: 3D printing and scanning technology can be expensive and requires specialized equipment and software.
In conclusion, calculating the volume of irregular shapes can be challenging, but there are several methods that can help. By mastering these methods, you can develop a deeper understanding of three-dimensional geometry and improve your problem-solving skills.
What is the most common method used to calculate the volume of irregular shapes?
+The most common method used to calculate the volume of irregular shapes is the decomposition method, which involves breaking down the shape into simpler components and calculating their volumes separately.
What is Cavalieri’s Principle, and how is it used to calculate the volume of irregular shapes?
+Cavalieri’s Principle states that if two shapes have equal altitudes and corresponding cross-sectional areas, then their volumes are equal. This principle can be used to calculate the volume of an irregular shape by comparing it to a simpler shape with known volume.
What is the method of indivisibles, and how is it used to calculate the volume of irregular shapes?
+The method of indivisibles involves dividing an irregular shape into an infinite number of infinitesimally small pieces, and then summing up their volumes to determine the total volume of the shape. This method is often used in calculus to calculate the volumes of complex shapes.
Related Terms:
- Volume of prisms worksheets
- Volume of L blocks
- Volume missing side Worksheet
- Volume of composite figures worksheet



