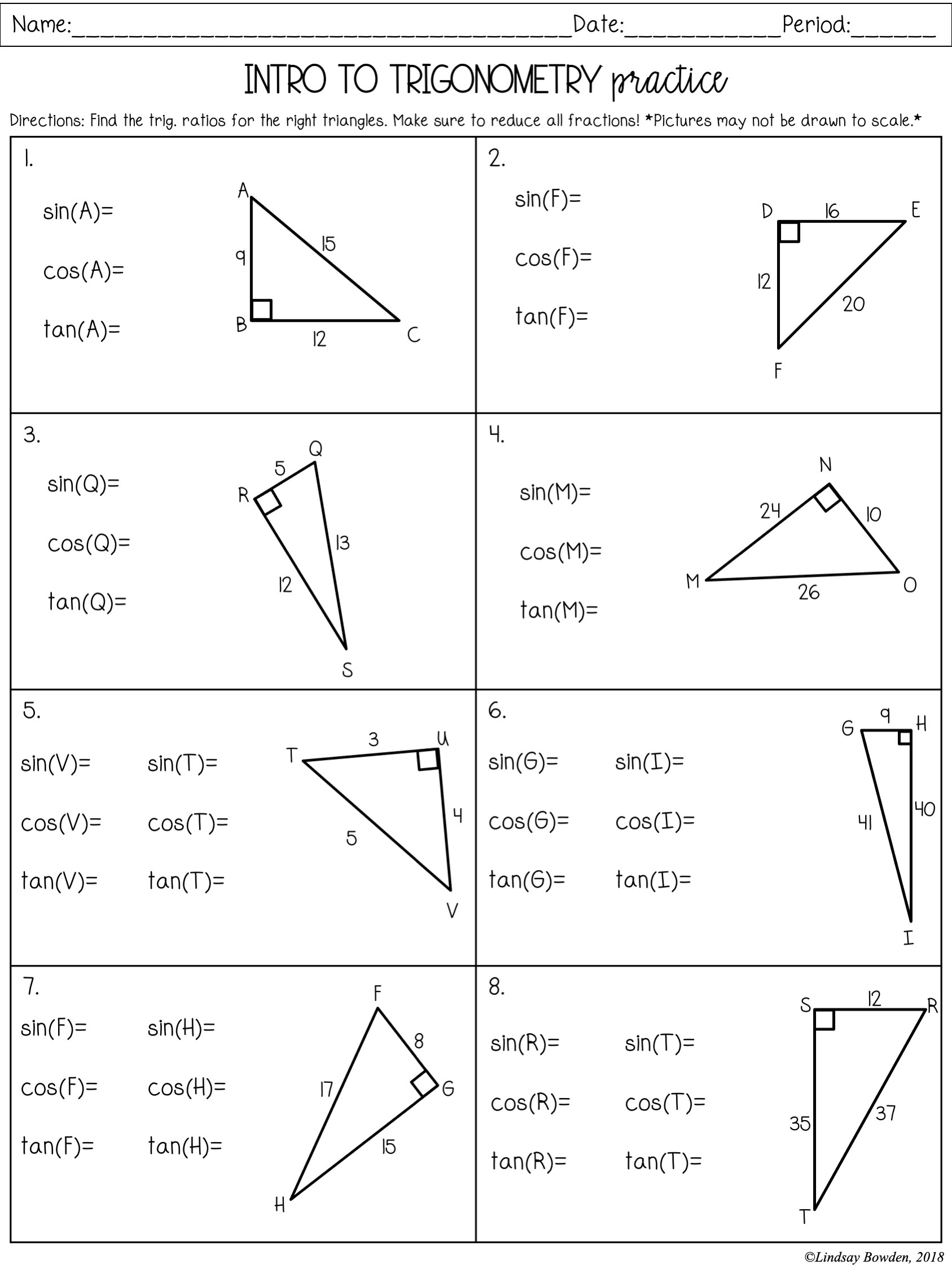
5 Ways to Master Properties of Multiplication

Understanding the Properties of Multiplication
Multiplication is a fundamental concept in mathematics that plays a crucial role in various mathematical operations. To master multiplication, it is essential to understand its properties, which are the rules that govern how numbers interact with each other when multiplied. In this blog post, we will explore five ways to master the properties of multiplication.
1. Commutative Property of Multiplication
The commutative property of multiplication states that the order of the numbers being multiplied does not change the result. This means that a × b = b × a. For example:
- 2 × 3 = 3 × 2 = 6
- 4 × 5 = 5 × 4 = 20
To master the commutative property, try rearranging the numbers in a multiplication problem to see if the result remains the same.
🤔 Note: The commutative property only applies to multiplication, not addition or subtraction.
2. Associative Property of Multiplication
The associative property of multiplication states that when multiplying three or more numbers, the order in which we multiply them does not change the result. This means that (a × b) × c = a × (b × c). For example:
- (2 × 3) × 4 = 2 × (3 × 4) = 24
- (5 × 2) × 3 = 5 × (2 × 3) = 30
To master the associative property, try rearranging the numbers in a multiplication problem to see if the result remains the same.
3. Distributive Property of Multiplication
The distributive property of multiplication states that when multiplying a number by a group of numbers, we can multiply each number in the group separately and then add the results. This means that a × (b + c) = a × b + a × c. For example:
- 2 × (3 + 4) = 2 × 3 + 2 × 4 = 6 + 8 = 14
- 5 × (2 + 6) = 5 × 2 + 5 × 6 = 10 + 30 = 40
To master the distributive property, try breaking down a multiplication problem into smaller parts and then combining the results.
4. Multiplication by Zero
Multiplication by zero is a fundamental concept in mathematics that states that any number multiplied by zero is equal to zero. This means that a × 0 = 0. For example:
- 2 × 0 = 0
- 5 × 0 = 0
To master multiplication by zero, remember that any number multiplied by zero will always result in zero.
5. Multiplication by One
Multiplication by one is another fundamental concept in mathematics that states that any number multiplied by one is equal to the number itself. This means that a × 1 = a. For example:
- 2 × 1 = 2
- 5 × 1 = 5
To master multiplication by one, remember that any number multiplied by one will always result in the number itself.
Practicing the Properties of Multiplication
To master the properties of multiplication, practice is essential. Here are some tips to help you practice:
- Use flashcards to quiz yourself on the properties of multiplication.
- Create multiplication charts to help you visualize the relationships between numbers.
- Practice solving multiplication problems using different numbers and scenarios.
- Use real-world examples to illustrate the properties of multiplication.

| Property | Example | Description |
|---|---|---|
| Commutative Property | 2 × 3 = 3 × 2 | The order of the numbers being multiplied does not change the result. |
| Associative Property | (2 × 3) × 4 = 2 × (3 × 4) | When multiplying three or more numbers, the order in which we multiply them does not change the result. |
| Distributive Property | 2 × (3 + 4) = 2 × 3 + 2 × 4 | When multiplying a number by a group of numbers, we can multiply each number in the group separately and then add the results. |
| Multiplication by Zero | 2 × 0 = 0 | Any number multiplied by zero is equal to zero. |
| Multiplication by One | 2 × 1 = 2 | Any number multiplied by one is equal to the number itself. |
Mastering the properties of multiplication takes time and practice, but with these tips and tricks, you can become a pro in no time. Remember to practice regularly and use real-world examples to illustrate the properties of multiplication.
In summary, mastering the properties of multiplication is essential to become proficient in mathematics. By understanding the commutative, associative, distributive, multiplication by zero, and multiplication by one properties, you can solve multiplication problems with ease and confidence. Remember to practice regularly and use real-world examples to reinforce your understanding of these properties.
What is the commutative property of multiplication?
+The commutative property of multiplication states that the order of the numbers being multiplied does not change the result. This means that a × b = b × a.
What is the associative property of multiplication?
+The associative property of multiplication states that when multiplying three or more numbers, the order in which we multiply them does not change the result. This means that (a × b) × c = a × (b × c).
What is the distributive property of multiplication?
+The distributive property of multiplication states that when multiplying a number by a group of numbers, we can multiply each number in the group separately and then add the results. This means that a × (b + c) = a × b + a × c.
Related Terms:
- Properties of multiplication Worksheet PDF