Mastering Rational Exponents Made Easy

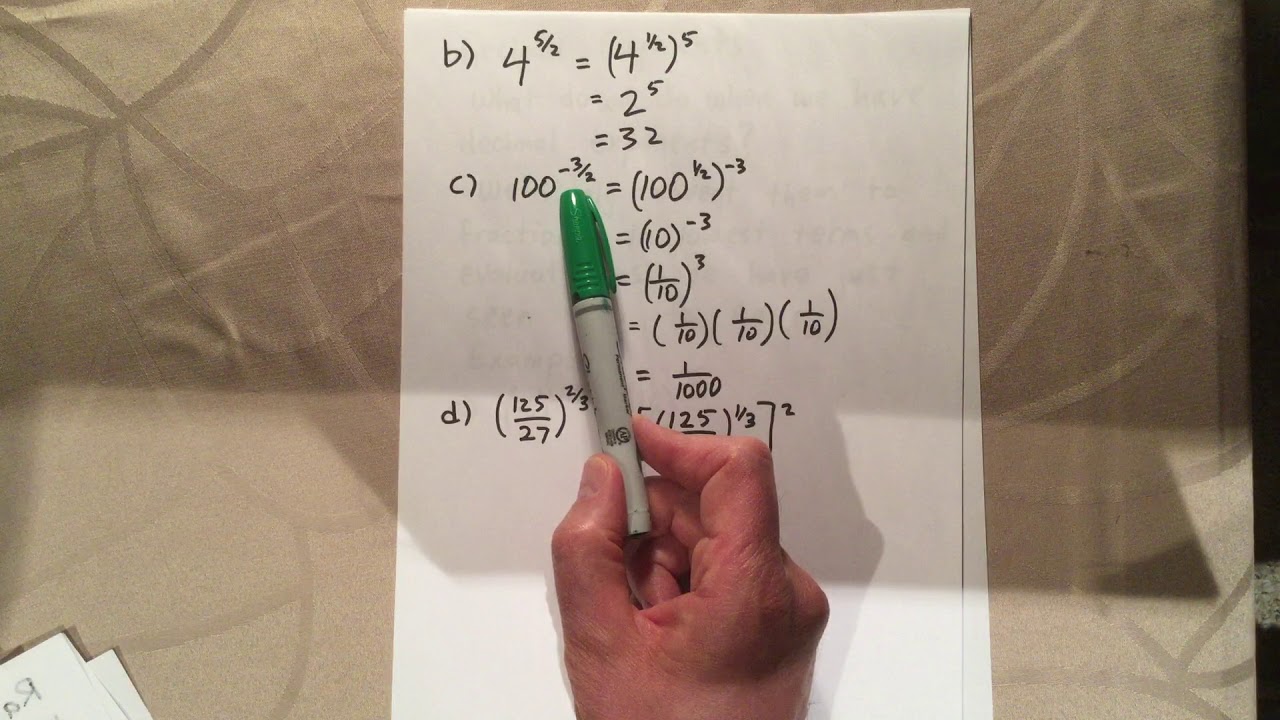
Understanding Rational Exponents

Rational exponents are a fundamental concept in mathematics, and they can be a bit tricky to grasp at first. However, with the right approach and explanation, mastering rational exponents can be made easy. In this blog post, we will delve into the world of rational exponents, explore their properties, and provide tips on how to work with them effortlessly.

What are Rational Exponents?

Rational exponents are exponents that are expressed as fractions, where the numerator is the power to which the base is raised, and the denominator is the root of the base. In other words, a rational exponent is a combination of a power and a root. For example, in the expression 2^{3/4}, the rational exponent is 3/4, which means that 2 is raised to the power of 3 and then taken to the 4th root.

Properties of Rational Exponents

Before we dive into the nitty-gritty of working with rational exponents, let’s explore some of their properties:

• Multiplication Property: When multiplying two numbers with rational exponents, we add the exponents. For example, 2^{1/3} \cdot 2^{2/3} = 2^{1/3 + 2/3} = 2^{3/3} = 2^1 = 2.
• Division Property: When dividing two numbers with rational exponents, we subtract the exponents. For example, 2^{2/3} \div 2^{1/3} = 2^{2/3 - 1/3} = 2^{1/3}.
• Power Property: When raising a number with a rational exponent to a power, we multiply the exponents. For example, (2^{1/3})^2 = 2^{1/3 \cdot 2} = 2^{2/3}.

Working with Rational Exponents

Now that we’ve explored the properties of rational exponents, let’s look at some examples of how to work with them:

• Simplifying Rational Exponents: To simplify a rational exponent, we can reduce the fraction to its lowest terms. For example, 2^{6/8} = 2^{3/4}.
• Adding and Subtracting Rational Exponents: When adding or subtracting rational exponents, we need to have the same base and the same denominator. For example, 2^{1/4} + 2^{1/4} = 2 \cdot 2^{1/4} = 2^{5/4}.
• Multiplying and Dividing Rational Exponents: When multiplying or dividing rational exponents, we can use the multiplication and division properties. For example, 2^{1/2} \cdot 2^{1/4} = 2^{1/2 + 1/4} = 2^{3/4}.

🤔 Note: When working with rational exponents, it's essential to keep the base and the exponent separate. This will help you avoid confusion and make calculations easier.

Common Mistakes to Avoid

When working with rational exponents, there are some common mistakes to avoid:

• Misapplying the Power Property: Be careful when applying the power property, as it can be easy to misapply it. For example, (2^{1/3})^2 \neq 2^{2/3}.
• Forgetting to Reduce Fractions: Always reduce fractions to their lowest terms to avoid confusion. For example, 2^{6/8} \neq 2^{3/4}.

Real-World Applications of Rational Exponents

Rational exponents have many real-world applications, including:

• Finance: Rational exponents are used in finance to calculate compound interest and investment returns.
• Science: Rational exponents are used in science to describe the growth of populations and the decay of radioactive materials.
• Engineering: Rational exponents are used in engineering to design electronic circuits and calculate stress on materials.

Conclusion

Mastering rational exponents takes practice and patience, but with the right approach and explanation, it can be made easy. By understanding the properties of rational exponents and how to work with them, you’ll be able to tackle complex problems with confidence. Remember to avoid common mistakes and keep practicing to become a pro at working with rational exponents.