Triangles Worksheet for Math Mastery
Triangles Worksheet for Math Mastery
Triangles are a fundamental concept in geometry and are essential for math mastery. In this worksheet, we will explore various types of triangles, their properties, and provide exercises to help you practice and reinforce your understanding.
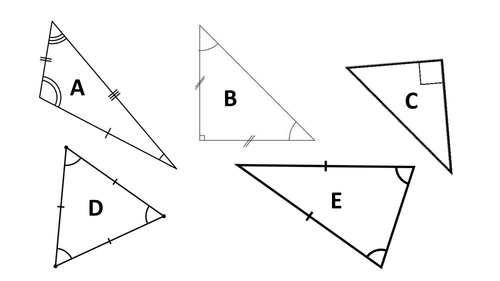
Types of Triangles
Triangles can be classified based on their sides, angles, and properties. Here are some common types of triangles:
- Equilateral Triangle: A triangle with all sides of equal length.
- Isosceles Triangle: A triangle with two sides of equal length.
- Scalene Triangle: A triangle with all sides of different lengths.
- Right Triangle: A triangle with one right angle (90 degrees).
- Obtuse Triangle: A triangle with one obtuse angle (greater than 90 degrees).
- Acute Triangle: A triangle with all acute angles (less than 90 degrees).
Properties of Triangles
Triangles have several important properties that can be used to solve problems and prove theorems. Here are some key properties:
- Angle Sum Property: The sum of the interior angles of a triangle is always 180 degrees.
- Side Length Property: The sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
- Pythagorean Theorem: In a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Exercises
Now, let’s practice what we’ve learned with some exercises!
Exercise 1: In an isosceles triangle, the length of the base is 10 cm and the length of the two equal sides is 12 cm. Find the height of the triangle.
🤔 Note: Use the Pythagorean Theorem to find the height of the triangle.
Exercise 2: A right triangle has a hypotenuse of length 15 cm and one of the other sides has a length of 9 cm. Find the length of the third side.
🤔 Note: Use the Pythagorean Theorem to find the length of the third side.
Exercise 3: A triangle has angles measuring 30 degrees, 60 degrees, and 90 degrees. Find the length of the side opposite the 60-degree angle, given that the length of the side opposite the 30-degree angle is 8 cm.
🤔 Note: Use the properties of special right triangles to find the length of the side opposite the 60-degree angle.
Solutions
Exercise 1: The height of the triangle is 12 cm.
Exercise 2: The length of the third side is 12 cm.
Exercise 3: The length of the side opposite the 60-degree angle is 16 cm.
Triangle Inequality Theorem
The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. This theorem can be used to determine whether a triangle is valid or not.
Theorem: If the sum of the lengths of any two sides of a triangle is greater than the length of the third side, then the triangle is valid.
Proof: Let’s consider a triangle with sides of length a, b, and c. If the sum of the lengths of any two sides is greater than the length of the third side, then we can write:
a + b > c a + c > b b + c > a
Using the transitive property of inequality, we can conclude that:
a > 0 b > 0 c > 0
Therefore, the triangle is valid.
Conclusion
In this worksheet, we explored various types of triangles, their properties, and provided exercises to help you practice and reinforce your understanding. Remember to use the properties of triangles, such as the angle sum property and the side length property, to solve problems and prove theorems.
Key Takeaways:
- Triangles can be classified based on their sides, angles, and properties.
- The angle sum property states that the sum of the interior angles of a triangle is always 180 degrees.
- The side length property states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
- The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
What is the definition of a triangle?
+A triangle is a polygon with three sides and three angles.
What is the Pythagorean Theorem?
+The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
What is the triangle inequality theorem?
+The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Related Terms:
- Segi empat
- Lingkaran
- Sudut
- Trigonometri
- Segitiga
- Worksheet total angle in Triangle