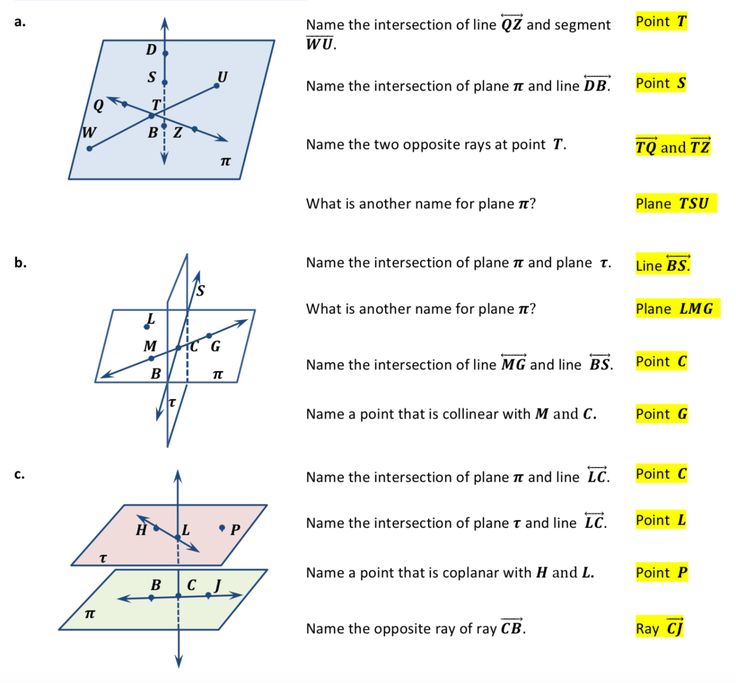
Points Lines and Planes Worksheet 1.1 Answer Key
Understanding Points, Lines, and Planes
In geometry, the foundation of all shapes and figures is built upon three fundamental concepts: points, lines, and planes. These elements are crucial in understanding more complex geometric concepts and are used extensively in various fields such as architecture, engineering, and design.
Definition of Points, Lines, and Planes
- Points: A point is a precise location in space, represented by a set of coordinates. It has no size or dimension, only position. Points are often denoted by capital letters.
- Lines: A line is a set of points that extend infinitely in two directions. It has length but no width or height. Lines can be straight or curved and are named by two points that lie on them.
- Planes: A plane is a flat surface that extends infinitely in all directions. It has length and width but no height. Planes can be named by three points that lie on them.
Key Concepts and Properties
- Intersecting Lines: Two lines intersect if they cross each other at exactly one point. The point where they intersect is called the point of intersection.
- Parallel Lines: Two lines are parallel if they lie in the same plane and do not intersect, no matter how far they are extended.
- Skew Lines: Two lines are skew if they do not intersect and are not parallel.
- Perpendicular Lines: Two lines are perpendicular if they intersect at a right angle (90 degrees).
- Collinear Points: Points are collinear if they lie on the same line.
- Coplanar Points: Points are coplanar if they lie in the same plane.
Points, Lines, and Planes Worksheet 1.1 Answer Key
Given the lack of specific questions in your prompt, I’ll create a sample worksheet with answers based on common questions related to points, lines, and planes.
Sample Questions and Answers:
Question: What is the definition of a point in geometry?
- Answer: A point is a precise location in space, represented by a set of coordinates. It has no size or dimension, only position.
Question: Can two lines intersect at more than one point?
- Answer: No, two lines can intersect at exactly one point.
Question: Define parallel lines.
- Answer: Parallel lines are lines that lie in the same plane and do not intersect, no matter how far they are extended.
Question: What are coplanar points?
- Answer: Coplanar points are points that lie in the same plane.
Question: Can a line be both parallel and perpendicular to another line?
- Answer: No, a line cannot be both parallel and perpendicular to another line. Parallel lines never intersect, while perpendicular lines intersect at a right angle.
Question: Name three points that lie on the plane of your desk.
- Answer: This will vary depending on the individual’s desk. For example, points A, B, and C, assuming A, B, and C are specific points identified on the desk.
Question: Define skew lines.
- Answer: Skew lines are lines that do not intersect and are not parallel.
Question: Can three points be collinear?
- Answer: Yes, three points can be collinear if they all lie on the same line.
Question: What is the difference between a line and a plane?
- Answer: A line has length but no width or height and extends infinitely in two directions. A plane is a flat surface that extends infinitely in all directions and has length and width but no height.
Question: Can a point lie on more than one line?
- Answer: Yes, a point can lie on more than one line. For example, the point of intersection of two lines.
📝 Note: The answers to these questions are based on fundamental geometric concepts and are provided as examples. Specific answers may vary depending on the context or specifics of the questions asked.
In conclusion, understanding the concepts of points, lines, and planes is essential for studying geometry and its applications. By grasping these fundamental elements, one can build a strong foundation for exploring more complex geometric ideas.
Related Terms:
- Geometry worksheet 1.1 answer key