Pyramid and Cone Volumes Worksheet Answers and Solutions
Understanding Pyramid and Cone Volumes
Pyramids and cones are two types of polyhedra that have unique properties and applications in mathematics and real-life scenarios. Calculating the volumes of these shapes is crucial in various fields, such as engineering, architecture, and physics. In this article, we will delve into the formulas and techniques used to calculate the volumes of pyramids and cones, along with some practice problems and solutions.
Pyramid Volume Formula
The volume of a pyramid is given by the formula:
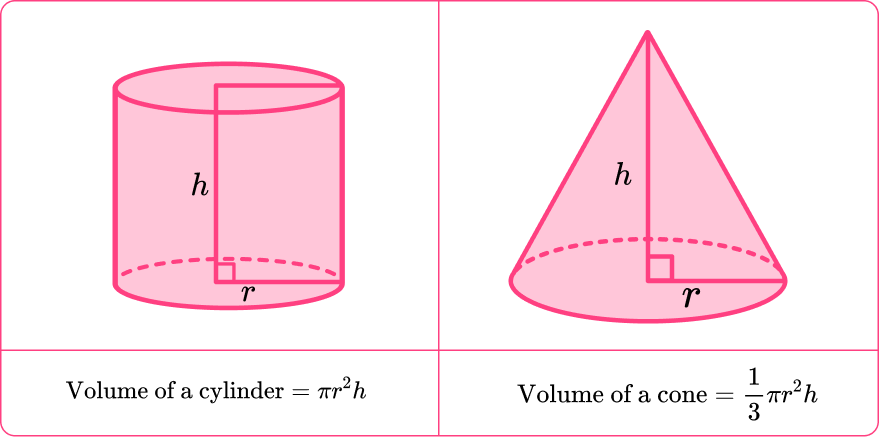
V = (1⁄3) × Base Area × Height
Where:
- V is the volume of the pyramid
- Base Area is the area of the pyramid’s base
- Height is the height of the pyramid
For example, if we have a pyramid with a square base of side length 4 cm and a height of 6 cm, the volume would be:
V = (1⁄3) × (4 × 4) × 6 V = (1⁄3) × 16 × 6 V = (1⁄3) × 96 V = 32
Cone Volume Formula
The volume of a cone is given by the formula:
V = (1⁄3) × π × Radius² × Height
Where:
- V is the volume of the cone
- π is a mathematical constant approximately equal to 3.14
- Radius is the radius of the cone’s base
- Height is the height of the cone
For instance, if we have a cone with a radius of 3 cm and a height of 8 cm, the volume would be:
V = (1⁄3) × π × (3)² × 8 V = (1⁄3) × 3.14 × 9 × 8 V = (1⁄3) × 3.14 × 72 V = (1⁄3) × 226.08 V = 75.36
Practice Problems and Solutions
Here are some practice problems to help you reinforce your understanding of pyramid and cone volumes:
- Find the volume of a pyramid with a triangular base of area 12 cm² and a height of 9 cm.
Solution: V = (1⁄3) × 12 × 9 V = (1⁄3) × 108 V = 36
- Find the volume of a cone with a radius of 2 cm and a height of 5 cm.
Solution: V = (1⁄3) × π × (2)² × 5 V = (1⁄3) × 3.14 × 4 × 5 V = (1⁄3) × 3.14 × 20 V = (1⁄3) × 62.8 V = 20.93
- Find the volume of a pyramid with a square base of side length 6 cm and a height of 12 cm.
Solution: V = (1⁄3) × (6 × 6) × 12 V = (1⁄3) × 36 × 12 V = (1⁄3) × 432 V = 144
- Find the volume of a cone with a radius of 4 cm and a height of 10 cm.
Solution: V = (1⁄3) × π × (4)² × 10 V = (1⁄3) × 3.14 × 16 × 10 V = (1⁄3) × 3.14 × 160 V = (1⁄3) × 502.4 V = 167.47
📝 Note: Make sure to check your calculations and units when solving problems.
Applications of Pyramid and Cone Volumes
Understanding the volumes of pyramids and cones is essential in various fields, such as:
- Engineering: designing buildings, bridges, and other structures
- Architecture: creating efficient and aesthetically pleasing buildings
- Physics: calculating the volumes of objects in motion
- Math: solving problems involving three-dimensional shapes
In conclusion, calculating the volumes of pyramids and cones is a fundamental concept in mathematics and has numerous applications in real-life scenarios. By mastering the formulas and techniques outlined in this article, you will be able to tackle a wide range of problems and appreciate the beauty of three-dimensional geometry.
What is the formula for the volume of a pyramid?
+
The formula for the volume of a pyramid is V = (1⁄3) × Base Area × Height.
What is the formula for the volume of a cone?
+
The formula for the volume of a cone is V = (1⁄3) × π × Radius² × Height.
Why is it important to understand the volumes of pyramids and cones?
+
Understanding the volumes of pyramids and cones is essential in various fields, such as engineering, architecture, physics, and math, as it helps in designing and solving problems involving three-dimensional shapes.