5 Ways to Solve Volume of Sphere and Hemisphere
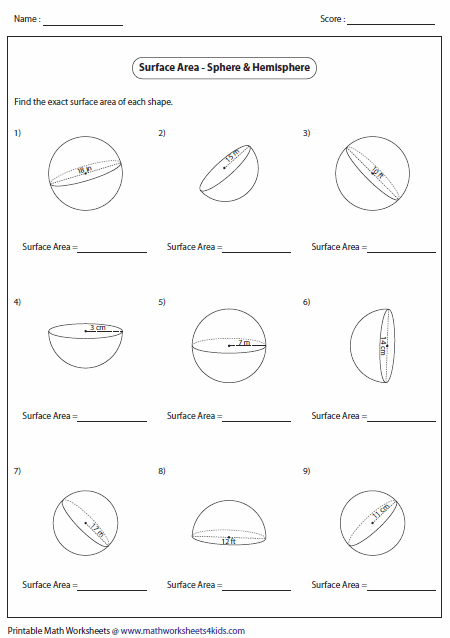
Understanding the Basics of Volume of Sphere and Hemisphere
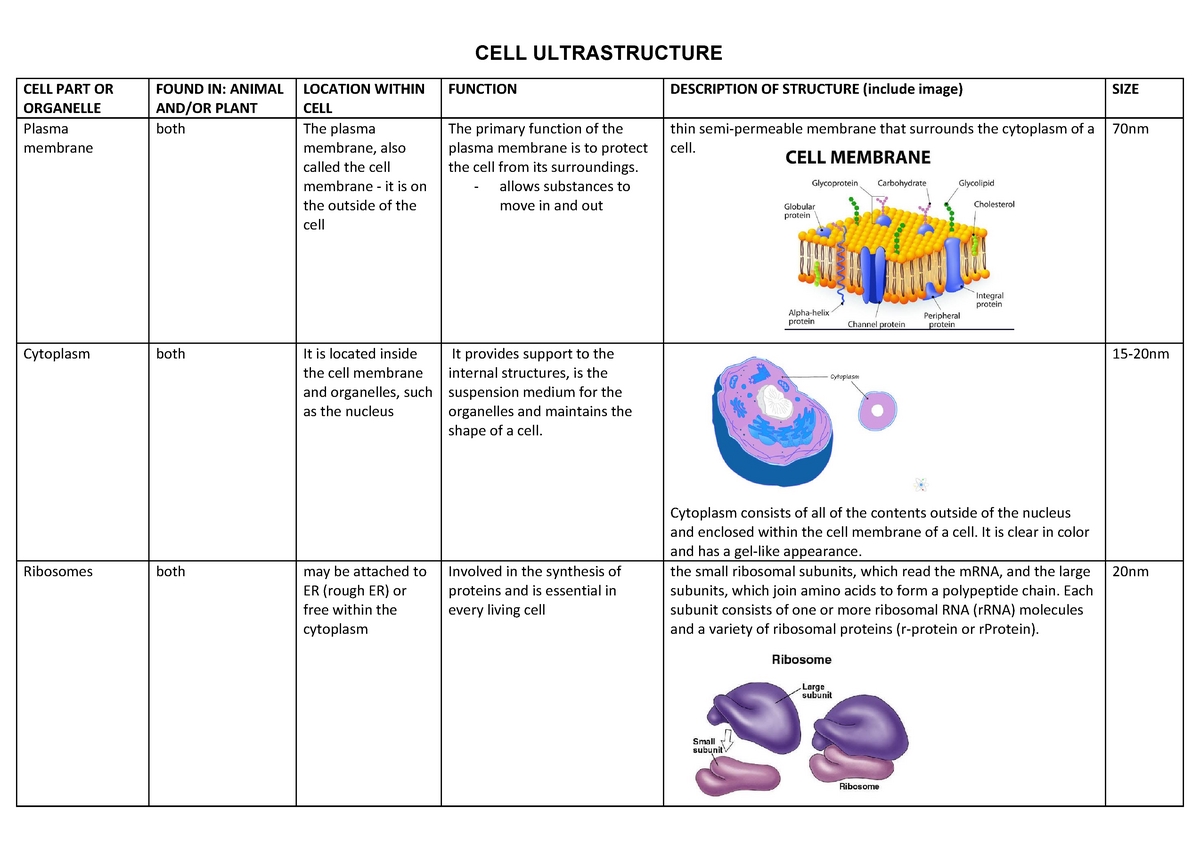
The volume of a sphere and hemisphere is a fundamental concept in geometry and mathematics. A sphere is a three-dimensional shape that is perfectly symmetrical about its center, and a hemisphere is half of a sphere. Calculating the volume of these shapes is crucial in various fields, including architecture, engineering, and design. In this article, we will explore five ways to solve the volume of a sphere and hemisphere.
Method 1: Using the Formula for the Volume of a Sphere
The formula for the volume of a sphere is:
V = (4⁄3)πr^3
where V is the volume, π is a mathematical constant approximately equal to 3.14, and r is the radius of the sphere.
To calculate the volume of a sphere, simply plug in the value of the radius into the formula. For example, if the radius of the sphere is 4 cm, the volume would be:
V = (4⁄3)π(4)^3 V = (4⁄3)π(64) V = (4⁄3)(3.14)(64) V = 268.08 cubic cm
Method 2: Using the Formula for the Volume of a Hemisphere
The formula for the volume of a hemisphere is:
V = (2⁄3)πr^3
where V is the volume, π is a mathematical constant approximately equal to 3.14, and r is the radius of the hemisphere.
To calculate the volume of a hemisphere, simply plug in the value of the radius into the formula. For example, if the radius of the hemisphere is 4 cm, the volume would be:
V = (2⁄3)π(4)^3 V = (2⁄3)π(64) V = (2⁄3)(3.14)(64) V = 134.04 cubic cm
Method 3: Using the Relationship Between the Volume of a Sphere and a Hemisphere
A hemisphere is half of a sphere, so the volume of a hemisphere is half the volume of a sphere. Therefore, we can calculate the volume of a hemisphere by dividing the volume of a sphere by 2.
For example, if the volume of a sphere is 268.08 cubic cm, the volume of the corresponding hemisphere would be:
V = 268.08 / 2 V = 134.04 cubic cm
Method 4: Using the Diameter Instead of the Radius
Sometimes, we may be given the diameter of a sphere or hemisphere instead of the radius. In this case, we can use the fact that the diameter is twice the radius to calculate the volume.
For example, if the diameter of a sphere is 8 cm, the radius would be:
r = 8 / 2 r = 4 cm
We can then use the formula for the volume of a sphere to calculate the volume:
V = (4⁄3)π(4)^3 V = (4⁄3)π(64) V = (4⁄3)(3.14)(64) V = 268.08 cubic cm
Method 5: Using a Calculator or Software
Finally, we can use a calculator or software to calculate the volume of a sphere or hemisphere. Many calculators and software programs, such as math software or 3D modeling software, have built-in formulas for calculating the volume of a sphere and hemisphere.
For example, we can use a calculator to calculate the volume of a sphere with a radius of 4 cm:
V = (4⁄3)π(4)^3 V ≈ 268.08 cubic cm
🤔 Note: When using a calculator or software, make sure to enter the correct values and units to get accurate results.
In conclusion, there are several ways to solve the volume of a sphere and hemisphere, including using formulas, relationships between shapes, and calculators or software. By understanding these different methods, we can choose the most convenient and accurate way to solve problems involving the volume of spheres and hemispheres.
What is the formula for the volume of a sphere?
+The formula for the volume of a sphere is V = (4⁄3)πr^3, where V is the volume, π is a mathematical constant approximately equal to 3.14, and r is the radius of the sphere.
How do I calculate the volume of a hemisphere?
+The formula for the volume of a hemisphere is V = (2⁄3)πr^3, where V is the volume, π is a mathematical constant approximately equal to 3.14, and r is the radius of the hemisphere. Alternatively, you can calculate the volume of a hemisphere by dividing the volume of a sphere by 2.
Can I use a calculator to calculate the volume of a sphere or hemisphere?
+Yes, many calculators and software programs have built-in formulas for calculating the volume of a sphere and hemisphere. Simply enter the correct values and units to get accurate results.