Volume And Surface Area Worksheets
Understanding Volume and Surface Area: A Comprehensive Guide
In mathematics, particularly in geometry, volume and surface area are two fundamental concepts that help us understand the properties of three-dimensional shapes. In this blog post, we will delve into the world of volume and surface area, exploring their definitions, formulas, and applications.
What is Volume?
Volume refers to the amount of space inside a three-dimensional shape. It is a measure of the capacity of a shape to hold or contain something. For example, the volume of a cube is the amount of space inside the cube, while the volume of a sphere is the amount of space inside the sphere.
What is Surface Area?
Surface area, on the other hand, refers to the total area of the surface of a three-dimensional shape. It is a measure of the total area of the shape’s exterior. For example, the surface area of a cube is the total area of its six faces, while the surface area of a sphere is the area of its curved surface.
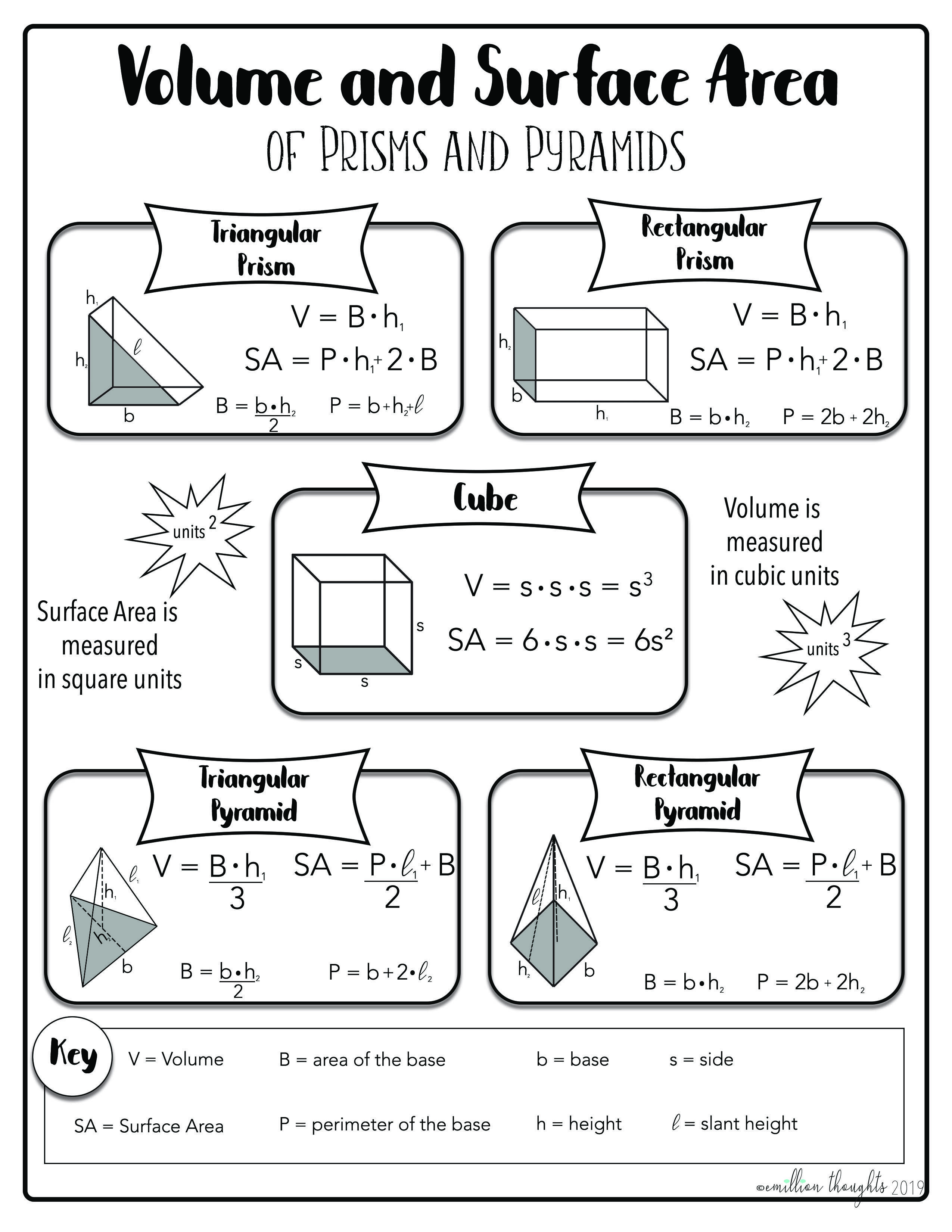
Formulas for Volume and Surface Area
Here are some common formulas for volume and surface area:
Volume Formulas:
- Cube: V = s^3 (where s is the length of the side)
- Rectangular Prism: V = lwh (where l is the length, w is the width, and h is the height)
- Sphere: V = (4⁄3)πr^3 (where r is the radius)
- Cylinder: V = πr^2h (where r is the radius and h is the height)
Surface Area Formulas:
- Cube: SA = 6s^2 (where s is the length of the side)
- Rectangular Prism: SA = 2lw + 2lh + 2wh (where l is the length, w is the width, and h is the height)
- Sphere: SA = 4πr^2 (where r is the radius)
- Cylinder: SA = 2πr^2 + 2πrh (where r is the radius and h is the height)
Volume and Surface Area Worksheets
To help you practice and reinforce your understanding of volume and surface area, here are some worksheets with exercises and problems:
Volume Worksheets:
- Find the volume of a cube with a side length of 5 cm.
- Find the volume of a rectangular prism with a length of 6 cm, a width of 4 cm, and a height of 2 cm.
- Find the volume of a sphere with a radius of 3 cm.
Surface Area Worksheets:
- Find the surface area of a cube with a side length of 4 cm.
- Find the surface area of a rectangular prism with a length of 8 cm, a width of 6 cm, and a height of 2 cm.
- Find the surface area of a sphere with a radius of 2 cm.
Real-World Applications of Volume and Surface Area
Volume and surface area have numerous real-world applications in various fields, including:
- Architecture: designing buildings and bridges
- Engineering: designing machines and mechanisms
- Physics: calculating the volume and surface area of objects in motion
- Biology: understanding the structure and function of living organisms
Common Mistakes to Avoid
When working with volume and surface area, here are some common mistakes to avoid:
- Confusing volume and surface area formulas
- Forgetting to square or cube units when calculating volume or surface area
- Not using the correct units of measurement
🚨 Note: Always double-check your calculations and make sure to use the correct units of measurement.
Conclusion
In conclusion, volume and surface area are two essential concepts in geometry that help us understand the properties of three-dimensional shapes. By mastering the formulas and applications of volume and surface area, you can develop a deeper understanding of the world around you and improve your problem-solving skills.
What is the difference between volume and surface area?
+Volume refers to the amount of space inside a three-dimensional shape, while surface area refers to the total area of the surface of a three-dimensional shape.
How do I calculate the volume of a sphere?
+The formula for the volume of a sphere is V = (4⁄3)πr^3, where r is the radius.
What are some real-world applications of volume and surface area?
+Volume and surface area have numerous real-world applications in various fields, including architecture, engineering, physics, and biology.