5 Types of Triangles to Know
Understanding the Different Types of Triangles
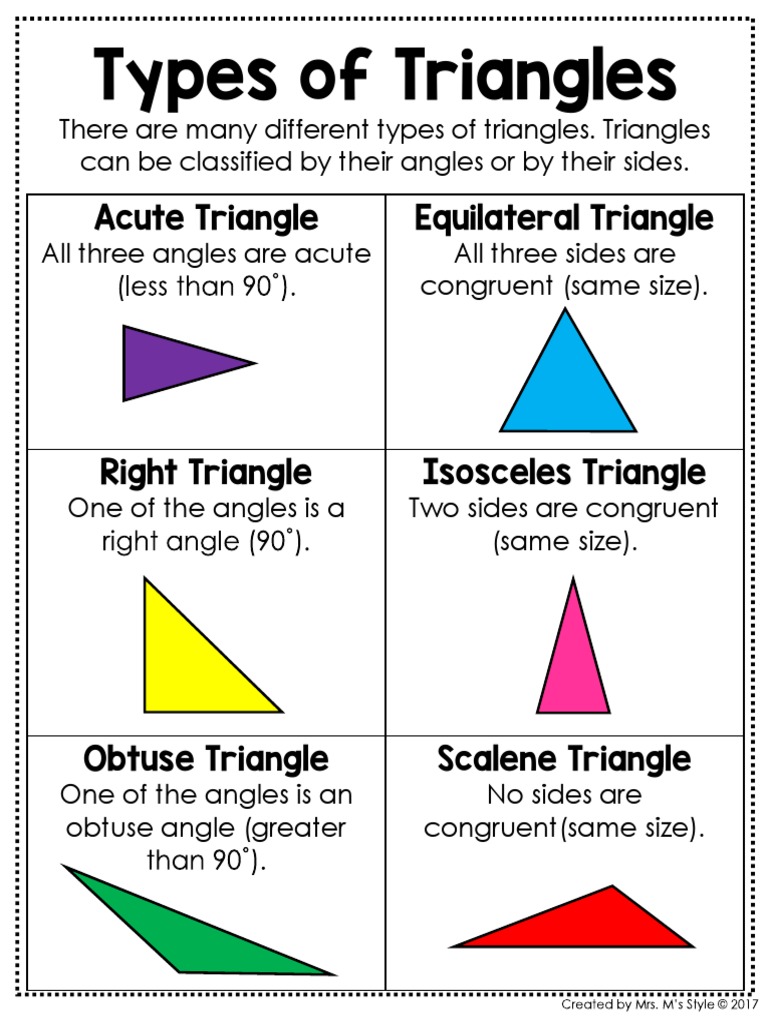
Triangles are one of the most basic and essential shapes in geometry. A triangle is a polygon with three sides, and it is the most stable shape in terms of structural integrity. There are several types of triangles, each with its unique characteristics and properties. In this article, we will explore five types of triangles that you should know.
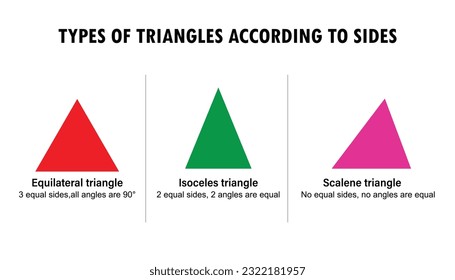
1. Equilateral Triangle
An equilateral triangle is a triangle with all sides of equal length. The internal angles of an equilateral triangle are all 60 degrees, making it a very symmetrical and balanced shape. Equilateral triangles have several unique properties, including:
- All sides are equal
- All internal angles are 60 degrees
- The triangle is symmetrical about its centroid (the point where the medians intersect)
📝 Note: Equilateral triangles are often used in art and design to create visually appealing and balanced compositions.
2. Isosceles Triangle
An isosceles triangle is a triangle with two sides of equal length. The internal angles of an isosceles triangle are not all equal, but the triangle is still symmetrical about its axis of symmetry (the line that bisects the triangle into two congruent halves). Isosceles triangles have several key characteristics, including:
- Two sides are equal
- The internal angles are not all equal
- The triangle is symmetrical about its axis of symmetry
3. Scalene Triangle
A scalene triangle is a triangle with all sides of different lengths. The internal angles of a scalene triangle are also all different, making it the most irregular of all triangle types. Scalene triangles have several notable properties, including:
- All sides are different lengths
- All internal angles are different
- The triangle has no axis of symmetry
📝 Note: Scalene triangles are often used in engineering and architecture to create stable and strong structures.
4. Right Triangle
A right triangle is a triangle with one internal angle that is 90 degrees (a “right angle”). Right triangles have several important properties, including:
- One internal angle is 90 degrees
- The triangle can be solved using trigonometric ratios (sine, cosine, and tangent)
- The triangle is often used in applications involving distance and angle calculations
5. Oblique Triangle
An oblique triangle is a triangle that is not a right triangle (i.e., it does not have any internal right angles). Oblique triangles can be either acute or obtuse, depending on the size of their internal angles. Oblique triangles have several key characteristics, including:
- No internal right angles
- The triangle can be either acute or obtuse
- The triangle has no special properties or symmetries
| Triangle Type | Description |
|---|---|
| Equilateral | All sides equal, all internal angles 60 degrees |
| Isosceles | Two sides equal, internal angles not all equal |
| Scalene | All sides different lengths, all internal angles different |
| Right | One internal angle 90 degrees, can be solved using trigonometry |
| Oblique | No internal right angles, can be acute or obtuse |
Understanding the different types of triangles is essential for success in mathematics, engineering, and many other fields. By knowing the unique properties and characteristics of each triangle type, you can solve problems more efficiently and effectively.
In this article, we have explored five types of triangles: equilateral, isosceles, scalene, right, and oblique. Each triangle type has its own set of properties and characteristics that make it unique and useful in different contexts. Whether you are a student, engineer, or simply someone interested in geometry, understanding the different types of triangles is an essential part of your mathematical toolkit.
What is the most stable type of triangle?
+The equilateral triangle is considered the most stable type of triangle due to its symmetrical shape and balanced internal angles.
What is the difference between an isosceles and a scalene triangle?
+An isosceles triangle has two sides of equal length, while a scalene triangle has all sides of different lengths.
What is the importance of right triangles in trigonometry?
+Right triangles are essential in trigonometry because they can be solved using trigonometric ratios (sine, cosine, and tangent), making them useful for calculating distances and angles.