Understanding Slopes: Identifying Types of Slope Worksheet
Understanding Slopes: A Comprehensive Guide
Slopes are a fundamental concept in mathematics, particularly in geometry and algebra. In simple terms, a slope refers to the measure of how steep a line is. It is a crucial concept in various fields, including physics, engineering, and economics. In this article, we will delve into the world of slopes, exploring different types of slopes, how to calculate them, and providing a worksheet to help you practice.
What is a Slope?
A slope is a measure of the steepness of a line. It is calculated as the ratio of the vertical change (rise) to the horizontal change (run) between two points on a line. The slope can be positive, negative, or zero, depending on the direction of the line.
Types of Slopes
There are several types of slopes, each with its unique characteristics. Here are some of the most common types of slopes:
- Positive Slope: A positive slope indicates that the line slopes upward from left to right. In other words, as the x-coordinate increases, the y-coordinate also increases.
- Negative Slope: A negative slope indicates that the line slopes downward from left to right. In other words, as the x-coordinate increases, the y-coordinate decreases.
- Zero Slope: A zero slope indicates that the line is horizontal, meaning that the y-coordinate remains constant as the x-coordinate changes.
- Undefined Slope: An undefined slope indicates that the line is vertical, meaning that the x-coordinate remains constant as the y-coordinate changes.
Calculating Slope
To calculate the slope of a line, you can use the following formula:
Slope (m) = (y2 - y1) / (x2 - x1)
where (x1, y1) and (x2, y2) are two points on the line.
For example, if you have two points (2, 3) and (4, 5), the slope would be:
m = (5 - 3) / (4 - 2) m = 2 / 2 m = 1
This means that the line has a positive slope of 1.
📝 Note: When calculating slope, make sure to subtract the y-coordinates and x-coordinates separately, and then divide the results.
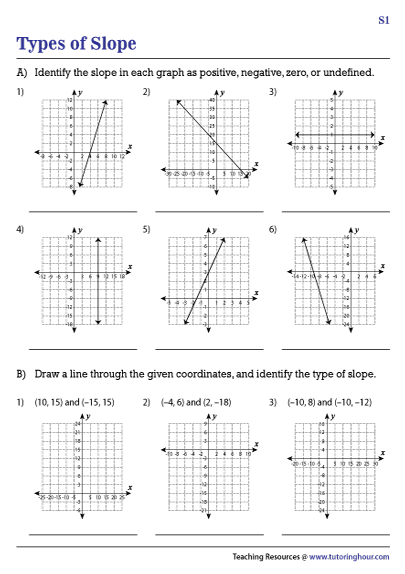
Identifying Types of Slope Worksheet
Here is a worksheet to help you practice identifying different types of slopes:

| Line | Slope | Type of Slope |
|---|---|---|
| y = 2x + 1 | 2 | Positive Slope |
| y = -3x - 2 | -3 | Negative Slope |
| y = 0x + 4 | 0 | Zero Slope |
| x = 2y + 1 | Undefined | Undefined Slope |
| y = 1/2x - 3 | 1/2 | Positive Slope |
| y = -2x + 5 | -2 | Negative Slope |
To complete the worksheet, identify the type of slope for each line by calculating the slope using the formula above.
Practicing with Examples
Here are a few examples to help you practice identifying types of slopes:
- Find the slope of the line passing through the points (1, 2) and (3, 4).
- Determine the type of slope of the line y = -2x + 1.
- Calculate the slope of the line passing through the points (-2, 3) and (1, 5).
By practicing with these examples, you can develop a deeper understanding of slopes and become proficient in identifying different types of slopes.
Understanding slopes is a fundamental concept in mathematics, and being able to identify different types of slopes is crucial in various fields. By mastering this concept, you can tackle more complex problems and become proficient in mathematics.
What is the formula for calculating slope?
+The formula for calculating slope is: Slope (m) = (y2 - y1) / (x2 - x1)
What is the difference between a positive and negative slope?
+A positive slope indicates that the line slopes upward from left to right, while a negative slope indicates that the line slopes downward from left to right.
What is an undefined slope?
+An undefined slope indicates that the line is vertical, meaning that the x-coordinate remains constant as the y-coordinate changes.
Related Terms:
- Types of slope Notes PDF
- Find the slope Worksheet
- Slope and y-intercept Worksheet
- Slope triangle worksheet
- Slope formula worksheet grade 8
- Rise and run worksheet pdf