Trigonometric Ratios and Finding Missing Sides Made Easy

Unlocking the Secrets of Trigonometric Ratios and Missing Sides
Trigonometry, a branch of mathematics, deals with the relationships between the sides and angles of triangles. It’s a fundamental concept in various fields, including physics, engineering, and navigation. In this article, we’ll delve into the world of trigonometric ratios and explore how to find missing sides of triangles with ease.
Understanding Trigonometric Ratios
Trigonometric ratios are relationships between the sides of a right-angled triangle. The three primary ratios are:
- Sine (sin): The ratio of the length of the side opposite the angle to the length of the hypotenuse.
- Cosine (cos): The ratio of the length of the side adjacent to the angle to the length of the hypotenuse.
- Tangent (tan): The ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
These ratios can be expressed as:
sin(A) = opposite side / hypotenuse cos(A) = adjacent side / hypotenuse tan(A) = opposite side / adjacent side
🤔 Note: It's essential to remember that these ratios only apply to right-angled triangles.
Reciprocal Ratios
In addition to the primary ratios, there are three reciprocal ratios:
- Cosecant (csc): The reciprocal of sine (1/sin)
- Secant (sec): The reciprocal of cosine (1/cos)
- Cotangent (cot): The reciprocal of tangent (1/tan)
These reciprocal ratios can be useful in certain situations, especially when dealing with trigonometric identities.
Pythagorean Identities
Pythagorean identities are essential in trigonometry. They help us relate the trigonometric ratios to each other. The most common Pythagorean identity is:
sin^2(A) + cos^2(A) = 1
This identity can be used to find the value of one trigonometric ratio if the other is known.
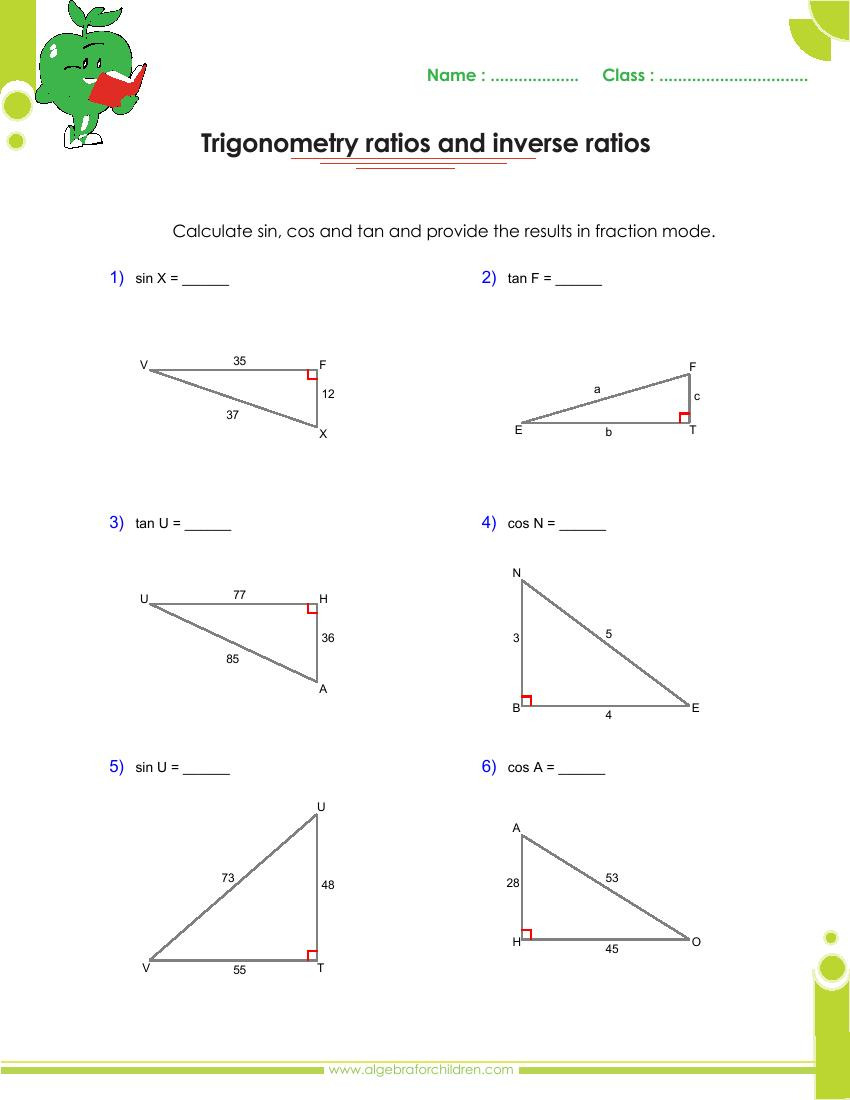
Finding Missing Sides
Now that we’ve covered the basics of trigonometric ratios, let’s move on to finding missing sides of triangles. We can use the trigonometric ratios to find the length of a side if we know the length of another side and the angle between them.
Method 1: Using the Sine Ratio
If we know the length of the opposite side and the angle, we can use the sine ratio to find the length of the hypotenuse:
hypotenuse = opposite side / sin(A)
Method 2: Using the Cosine Ratio
If we know the length of the adjacent side and the angle, we can use the cosine ratio to find the length of the hypotenuse:
hypotenuse = adjacent side / cos(A)
Method 3: Using the Tangent Ratio
If we know the length of the opposite side and the adjacent side, we can use the tangent ratio to find the angle:
tan(A) = opposite side / adjacent side
We can then use the angle to find the length of the hypotenuse using the sine or cosine ratio.
Example Problems
Let’s try some example problems to solidify our understanding of trigonometric ratios and finding missing sides.
Example 1:
In a right-angled triangle, the length of the opposite side is 3 inches, and the angle is 30 degrees. Find the length of the hypotenuse.
Using the sine ratio, we can find the length of the hypotenuse:
hypotenuse = 3 inches / sin(30) = 3 inches / 0.5 = 6 inches
Example 2:
In a right-angled triangle, the length of the adjacent side is 4 inches, and the angle is 45 degrees. Find the length of the hypotenuse.
Using the cosine ratio, we can find the length of the hypotenuse:
hypotenuse = 4 inches / cos(45) = 4 inches / 0.707 = 5.66 inches
Common Trigonometric Values
Here are some common trigonometric values that you should memorize:
| Angle | Sine | Cosine | Tangent |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1⁄2 | √3/2 | 1/√3 |
| 45° | 1/√2 | 1/√2 | 1 |
| 60° | √3/2 | 1⁄2 | √3 |
| 90° | 1 | 0 | undefined |
These values will come in handy when solving trigonometric problems.
Trigonometry is a fascinating subject that deals with the relationships between the sides and angles of triangles. By understanding trigonometric ratios and how to find missing sides, you’ll be able to solve a wide range of problems in various fields.
Remember to practice regularly and use the formulas and identities to become more comfortable with trigonometric calculations.
What is the difference between sine, cosine, and tangent?
+Sine, cosine, and tangent are three primary trigonometric ratios that relate the sides of a right-angled triangle. Sine is the ratio of the length of the side opposite the angle to the length of the hypotenuse. Cosine is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. Tangent is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
How do I find the length of a missing side in a right-angled triangle?
+To find the length of a missing side in a right-angled triangle, you can use the trigonometric ratios (sine, cosine, and tangent) along with the known sides and angles. For example, if you know the length of the opposite side and the angle, you can use the sine ratio to find the length of the hypotenuse.
What are some common trigonometric values that I should memorize?
+Some common trigonometric values that you should memorize include the values for 0°, 30°, 45°, 60°, and 90°. These values will come in handy when solving trigonometric problems.