5 Ways to Solve Literal Equations Easily

Understanding Literal Equations
Literal equations are a type of algebraic equation that involves variables and constants, but unlike linear equations, they can be more complex and involve multiple variables. These equations are used to solve problems that require finding the value of one variable in terms of another variable or variables. In this blog post, we will discuss 5 ways to solve literal equations easily.
Method 1: Isolate the Variable by Adding or Subtracting the Same Value
One of the simplest ways to solve literal equations is by isolating the variable by adding or subtracting the same value. This method involves moving the constant term to one side of the equation by performing the opposite operation.
For example, consider the equation: 2x + 5 = 11
To solve for x, we need to isolate the variable x. We can do this by subtracting 5 from both sides of the equation:
2x + 5 - 5 = 11 - 5 2x = 6
Next, we can divide both sides of the equation by 2 to solve for x:
2x / 2 = 6 / 2 x = 3
📝 Note: When adding or subtracting the same value, make sure to perform the operation on both sides of the equation to maintain the equality.
Method 2: Multiply or Divide Both Sides by the Same Value
Another way to solve literal equations is by multiplying or dividing both sides of the equation by the same value. This method involves getting rid of the coefficient of the variable by performing the opposite operation.
For example, consider the equation: 4x = 28
To solve for x, we can divide both sides of the equation by 4:
4x / 4 = 28 / 4 x = 7
Alternatively, we can also multiply both sides of the equation by 1⁄4:
(1⁄4) * 4x = (1⁄4) * 28 x = 7
📝 Note: When multiplying or dividing both sides of the equation, make sure to perform the operation on both sides of the equation to maintain the equality.
Method 3: Use the Distributive Property to Expand and Simplify
Literal equations can also be solved using the distributive property, which states that a(b + c) = ab + ac. This method involves expanding and simplifying the equation to isolate the variable.
For example, consider the equation: 2(x + 3) = 12
To solve for x, we can expand the equation using the distributive property:
2x + 6 = 12
Next, we can subtract 6 from both sides of the equation:
2x = 6
Finally, we can divide both sides of the equation by 2:
x = 3
📝 Note: When using the distributive property, make sure to expand and simplify the equation carefully to avoid errors.
Method 4: Use the Inverse Operation to Get Rid of the Coefficient
Another way to solve literal equations is by using the inverse operation to get rid of the coefficient. This method involves using the opposite operation to eliminate the coefficient.
For example, consider the equation: x/2 = 5
To solve for x, we can use the inverse operation of division, which is multiplication. We can multiply both sides of the equation by 2:
(x/2) * 2 = 5 * 2 x = 10
Alternatively, we can also use the inverse operation of multiplication, which is division. We can divide both sides of the equation by 1⁄2:
x / (1⁄2) = 5 / (1⁄2) x = 10
📝 Note: When using the inverse operation, make sure to use the correct operation to eliminate the coefficient.
Method 5: Use a Table to Organize and Solve the Equation
Finally, we can use a table to organize and solve literal equations. This method involves creating a table with columns for the variable, coefficient, and constant term.
For example, consider the equation: 3x - 2 = 11
We can create a table with the following columns:
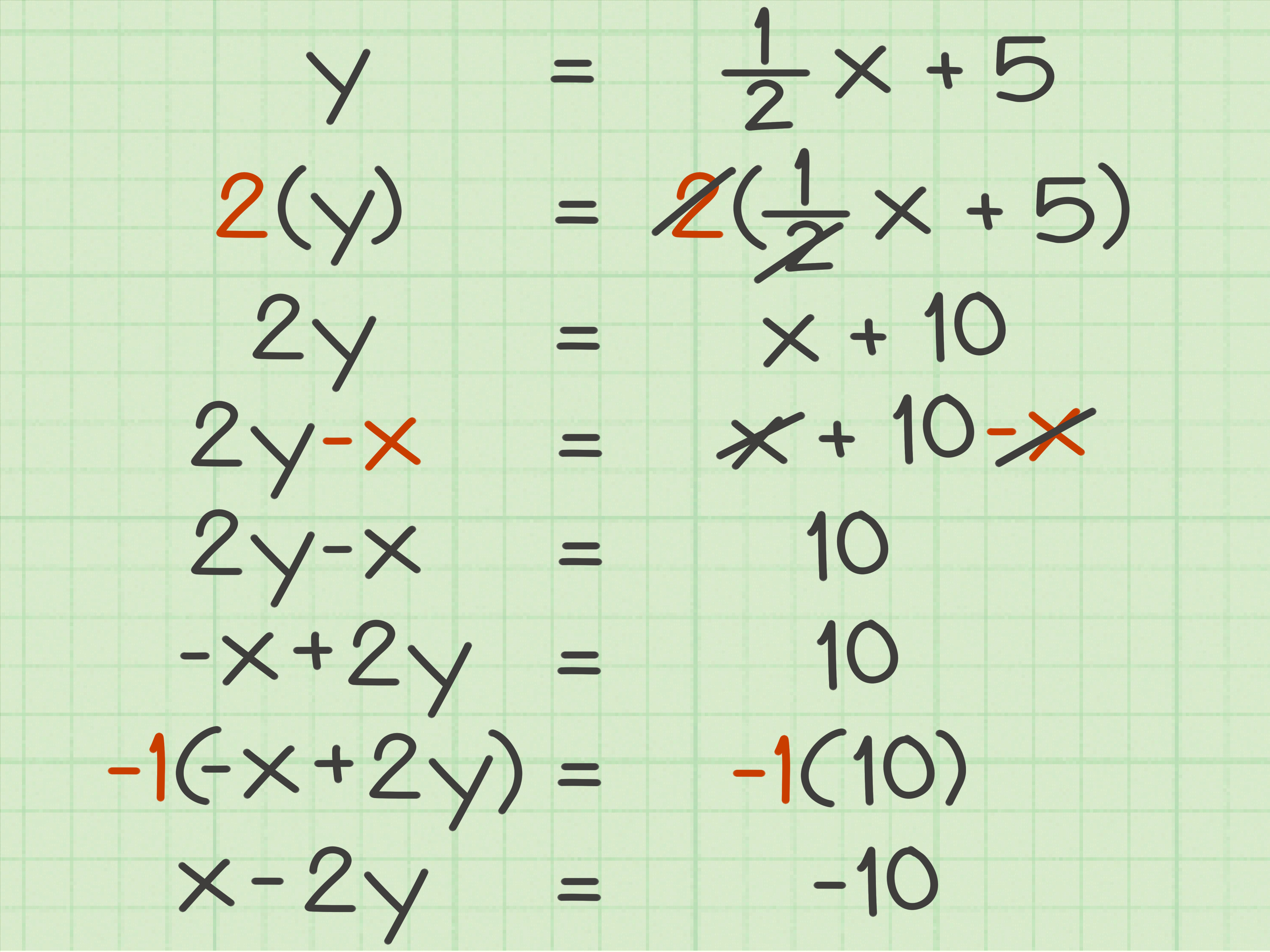
| Variable | Coefficient | Constant Term |
|---|---|---|
| x | 3 | -2 |
To solve for x, we can add 2 to both sides of the equation and then divide both sides by 3:
3x - 2 + 2 = 11 + 2 3x = 13
x = 13⁄3
We can then update the table with the new values:
| Variable | Coefficient | Constant Term |
|---|---|---|
| x | 1 | 13⁄3 |
Using a table to organize and solve literal equations can be helpful when dealing with complex equations.
📝 Note: When using a table, make sure to update the values carefully to avoid errors.
Wrapping Up
Solving literal equations can be challenging, but with the right strategies and techniques, it can be made easier. In this blog post, we discussed 5 ways to solve literal equations easily, including isolating the variable by adding or subtracting the same value, multiplying or dividing both sides by the same value, using the distributive property to expand and simplify, using the inverse operation to get rid of the coefficient, and using a table to organize and solve the equation. By mastering these methods, you can become proficient in solving literal equations and improve your math skills.
What is a literal equation?
+A literal equation is a type of algebraic equation that involves variables and constants, but unlike linear equations, they can be more complex and involve multiple variables.
What is the distributive property?
+The distributive property is a mathematical property that states that a(b + c) = ab + ac. It is used to expand and simplify equations.
What is the inverse operation?
+The inverse operation is the opposite operation of a given operation. For example, the inverse operation of addition is subtraction, and the inverse operation of multiplication is division.