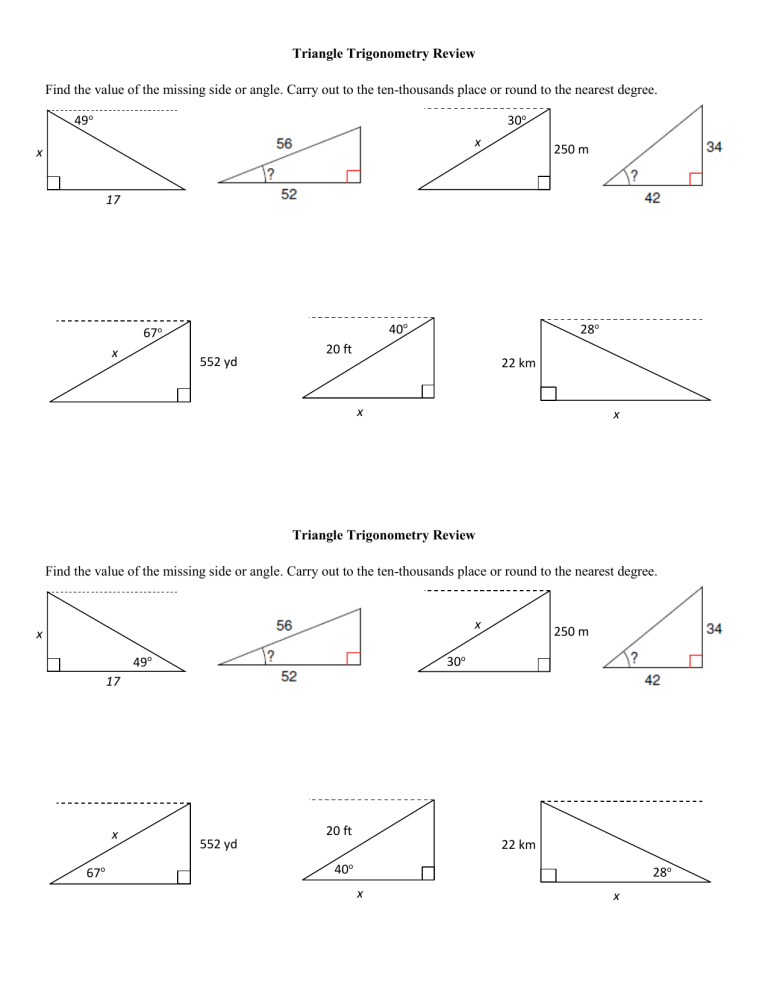
Solve Triangles Easily With Trig Word Problems Worksheet
Mastering Trigonometry: A Comprehensive Guide to Solving Triangles
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. It is a fundamental subject that has numerous applications in various fields, including physics, engineering, navigation, and more. One of the most effective ways to learn trigonometry is by practicing trig word problems, which involve solving triangles using trigonometric ratios and formulas. In this article, we will explore the basics of trigonometry, provide a step-by-step guide to solving triangles, and offer a trig word problems worksheet to help you practice and reinforce your understanding.
Understanding Trigonometric Ratios
Trigonometric ratios are the building blocks of trigonometry. They are used to describe the relationships between the sides and angles of triangles. The three most common trigonometric ratios are:
- Sine (sin): The ratio of the length of the side opposite a given angle to the length of the hypotenuse.
- Cosine (cos): The ratio of the length of the side adjacent to a given angle to the length of the hypotenuse.
- Tangent (tan): The ratio of the length of the side opposite a given angle to the length of the side adjacent to that angle.
These ratios can be expressed mathematically as:
sin(A) = opposite side / hypotenuse cos(A) = adjacent side / hypotenuse tan(A) = opposite side / adjacent side
Solving Triangles: A Step-by-Step Guide
Solving triangles involves using trigonometric ratios and formulas to find the unknown sides and angles of a triangle. Here’s a step-by-step guide to solving triangles:
- Read the problem carefully: Understand what information is given and what needs to be found.
- Draw a diagram: Sketch the triangle and label the known sides and angles.
- Identify the type of triangle: Determine if the triangle is a right triangle, oblique triangle, or equilateral triangle.
- Choose the correct trigonometric ratio: Select the appropriate trigonometric ratio based on the given information and the type of triangle.
- Apply the trigonometric ratio: Use the chosen trigonometric ratio to find the unknown side or angle.
- Check your answer: Verify your solution by checking if the answer is reasonable and makes sense in the context of the problem.
Trig Word Problems Worksheet
Practice makes perfect! Here’s a trig word problems worksheet to help you reinforce your understanding of solving triangles:
Problem 1 In a right triangle, the length of the hypotenuse is 10 cm, and the length of one leg is 6 cm. Find the length of the other leg.
Problem 2 In a triangle, the measure of one angle is 60°, and the length of the side opposite that angle is 8 cm. Find the length of the side adjacent to that angle.
Problem 3 A surveyor is measuring the distance between two points on a map. If the angle of elevation is 30°, and the distance between the two points is 200 meters, find the height of the surveyor’s instrument above the ground.
Problem 4 In a right triangle, the length of one leg is 3 cm, and the length of the other leg is 4 cm. Find the length of the hypotenuse.
Problem 5 A ship is sailing towards a lighthouse, which is 20 km away. If the angle of elevation of the lighthouse is 45°, find the height of the lighthouse.
📝 Note: Use a calculator to check your answers, and round your solutions to the nearest whole number or decimal place.
Common Trig Formulas and Identities
Here are some common trig formulas and identities that you may find useful when solving triangles:
- Pythagorean identity: sin²(A) + cos²(A) = 1
- Sum and difference formulas: sin(A + B) = sin(A)cos(B) + cos(A)sin(B)
- Double-angle formulas: sin(2A) = 2sin(A)cos(A)
- Half-angle formulas: sin(A/2) = ±√((1 - cos(A))/2)
Tips and Tricks
- Use a diagram: Always draw a diagram to visualize the problem and identify the given information.
- Check your units: Make sure to check your units and ensure that they are consistent throughout the problem.
- Use trig tables or a calculator: Use trig tables or a calculator to find the values of trigonometric ratios and functions.
- Practice, practice, practice: The more you practice solving triangles, the more confident you will become in using trigonometric ratios and formulas.
Without a summary, you will be able to solve triangles easily with the help of this guide and practice worksheet. Remember to practice regularly and use online resources to reinforce your understanding of trigonometry.
What is the difference between sine, cosine, and tangent?
+Sine, cosine, and tangent are three different trigonometric ratios that describe the relationships between the sides and angles of triangles. Sine is the ratio of the length of the side opposite a given angle to the length of the hypotenuse, cosine is the ratio of the length of the side adjacent to a given angle to the length of the hypotenuse, and tangent is the ratio of the length of the side opposite a given angle to the length of the side adjacent to that angle.
How do I choose the correct trigonometric ratio to use in a problem?
+To choose the correct trigonometric ratio, identify the given information and the type of triangle. Then, select the trigonometric ratio that corresponds to the given information and the type of triangle. For example, if you are given the length of the hypotenuse and the length of one leg, you would use the sine ratio.
What is the Pythagorean identity, and how is it used in trigonometry?
+The Pythagorean identity is a fundamental concept in trigonometry that states sin²(A) + cos²(A) = 1. This identity is used to find the value of one trigonometric ratio when the value of the other is known. For example, if you know the value of sine, you can use the Pythagorean identity to find the value of cosine.
Related Terms:
- Trigonometry Word Problems worksheets pdf