Triangle Area Worksheet with Solutions and Examples

Triangle Area Worksheet with Solutions and Examples
Calculating the area of a triangle is a fundamental concept in geometry and trigonometry. It is used to determine the size of the triangle, which can be useful in various mathematical and real-world applications. In this worksheet, we will provide you with examples and solutions to help you understand how to calculate the area of a triangle.
What is the Formula for the Area of a Triangle?
The formula for the area of a triangle is:
Area = (base × height) / 2
This formula is used when the base and height of the triangle are known. The base is the side of the triangle that is perpendicular to the height.
Example 1: Finding the Area of a Triangle with a Known Base and Height
Find the area of a triangle with a base of 5 cm and a height of 6 cm.
📝 Note: To find the area, we will use the formula: Area = (base × height) / 2
Solution:
Area = (5 cm × 6 cm) / 2 Area = 30 cm² / 2 Area = 15 cm²
Example 2: Finding the Area of a Triangle with a Known Base and Angle
Find the area of a triangle with a base of 8 cm and an angle of 60°. The height of the triangle is unknown.
📝 Note: To find the area, we will use the formula: Area = (base × height) / 2. Since the height is unknown, we will use trigonometry to find it.
Solution:
First, we need to find the height of the triangle using trigonometry:
sin(60°) = opposite side (height) / hypotenuse (base) sin(60°) = height / 8 cm height = 8 cm × sin(60°) height ≈ 6.93 cm
Now that we have the height, we can find the area:
Area = (base × height) / 2 Area = (8 cm × 6.93 cm) / 2 Area ≈ 27.48 cm²
Example 3: Finding the Area of a Triangle with Three Known Sides
Find the area of a triangle with sides of 7 cm, 8 cm, and 9 cm.
📝 Note: To find the area, we will use Heron's formula: Area = √(s(s - a)(s - b)(s - c)), where s is the semi-perimeter and a, b, and c are the sides of the triangle.
Solution:
First, we need to find the semi-perimeter:
s = (a + b + c) / 2 s = (7 cm + 8 cm + 9 cm) / 2 s = 12 cm
Now, we can use Heron’s formula to find the area:
Area = √(s(s - a)(s - b)(s - c)) Area = √(12 cm(12 cm - 7 cm)(12 cm - 8 cm)(12 cm - 9 cm)) Area ≈ 26.83 cm²
Table: Summary of Triangle Area Formulas
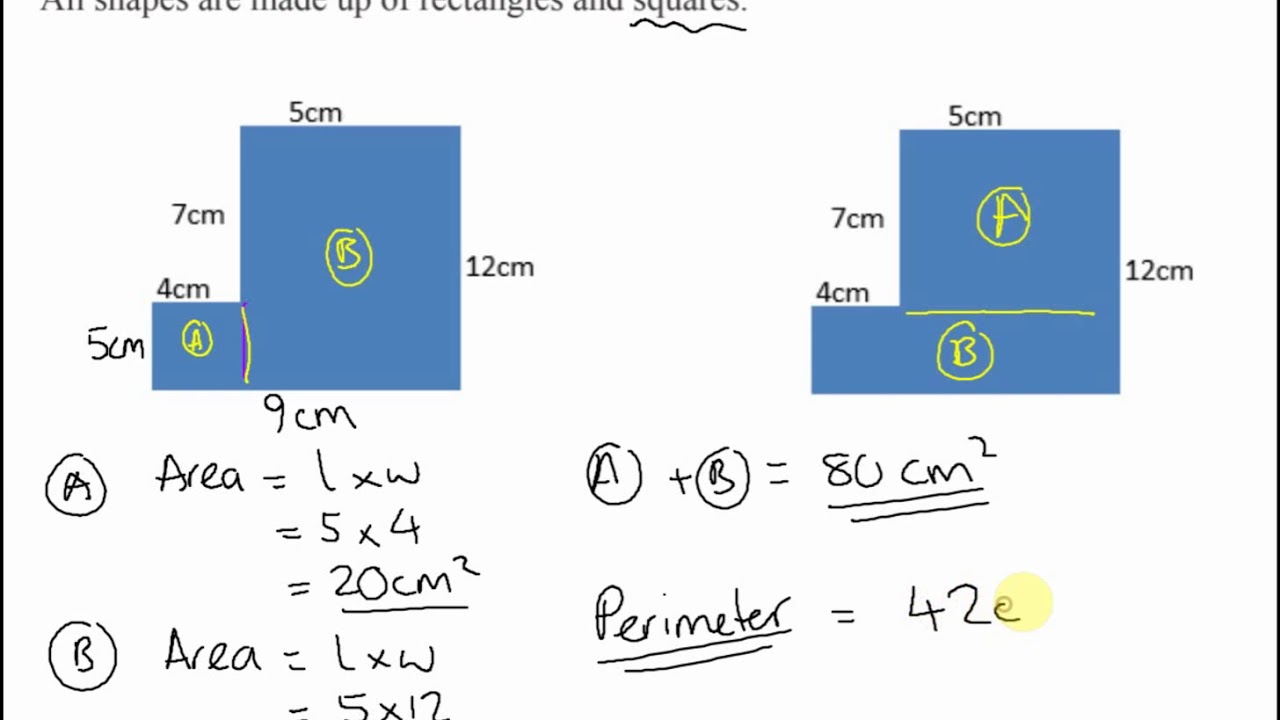
| Formula | Description |
|---|---|
| Area = (base × height) / 2 | Used when the base and height are known. |
| Area = (base × height) / 2 (using trigonometry) | Used when the base and angle are known. |
| Area = √(s(s - a)(s - b)(s - c)) (Heron’s formula) | Used when all three sides are known. |
Conclusion:
Calculating the area of a triangle can be done using various formulas, depending on the information provided. By understanding these formulas and practicing with examples, you can become proficient in finding the area of triangles.
Frequently Asked Questions:
What is the formula for the area of a triangle?
+The formula for the area of a triangle is: Area = (base × height) / 2.
What if I don’t know the height of the triangle?
+If you don’t know the height, you can use trigonometry to find it, or use Heron’s formula if all three sides are known.
What is Heron’s formula?
+Heron’s formula is a formula used to find the area of a triangle when all three sides are known: Area = √(s(s - a)(s - b)(s - c)), where s is the semi-perimeter and a, b, and c are the sides of the triangle.
Related Terms:
- Area of compound shapes worksheet
- Worksheet total angle in Triangle
- The area of triangle
- Perimeter worksheet grade 3