Translations Geometry Worksheet Solutions

Translations in Geometry: Understanding the Basics
In geometry, a translation is a type of transformation that involves moving a shape or an object from one position to another without changing its size, shape, or orientation. In this blog post, we will explore the concept of translations, provide solutions to common problems, and offer tips for understanding this fundamental concept in geometry.
What is a Translation in Geometry?
A translation is a transformation that moves a shape or an object from one position to another by sliding it along a straight line. This line is called the translation vector. The translation vector defines the direction and distance of the translation. When a shape is translated, its size and shape remain the same, but its position changes.
How to Perform a Translation
To perform a translation, you need to know the translation vector, which is usually represented by an arrow. The arrow points in the direction of the translation, and its length represents the distance of the translation. Here’s a step-by-step guide to performing a translation:
- Identify the translation vector.
- Draw an arrow representing the translation vector.
- Place the tail of the arrow at the starting point of the shape.
- Move the shape along the arrow, keeping it parallel to the original shape.
- Draw the translated shape at the new position.
Examples of Translations
Here are a few examples of translations:
- Example 1: Translate a triangle 3 units to the right and 2 units up.
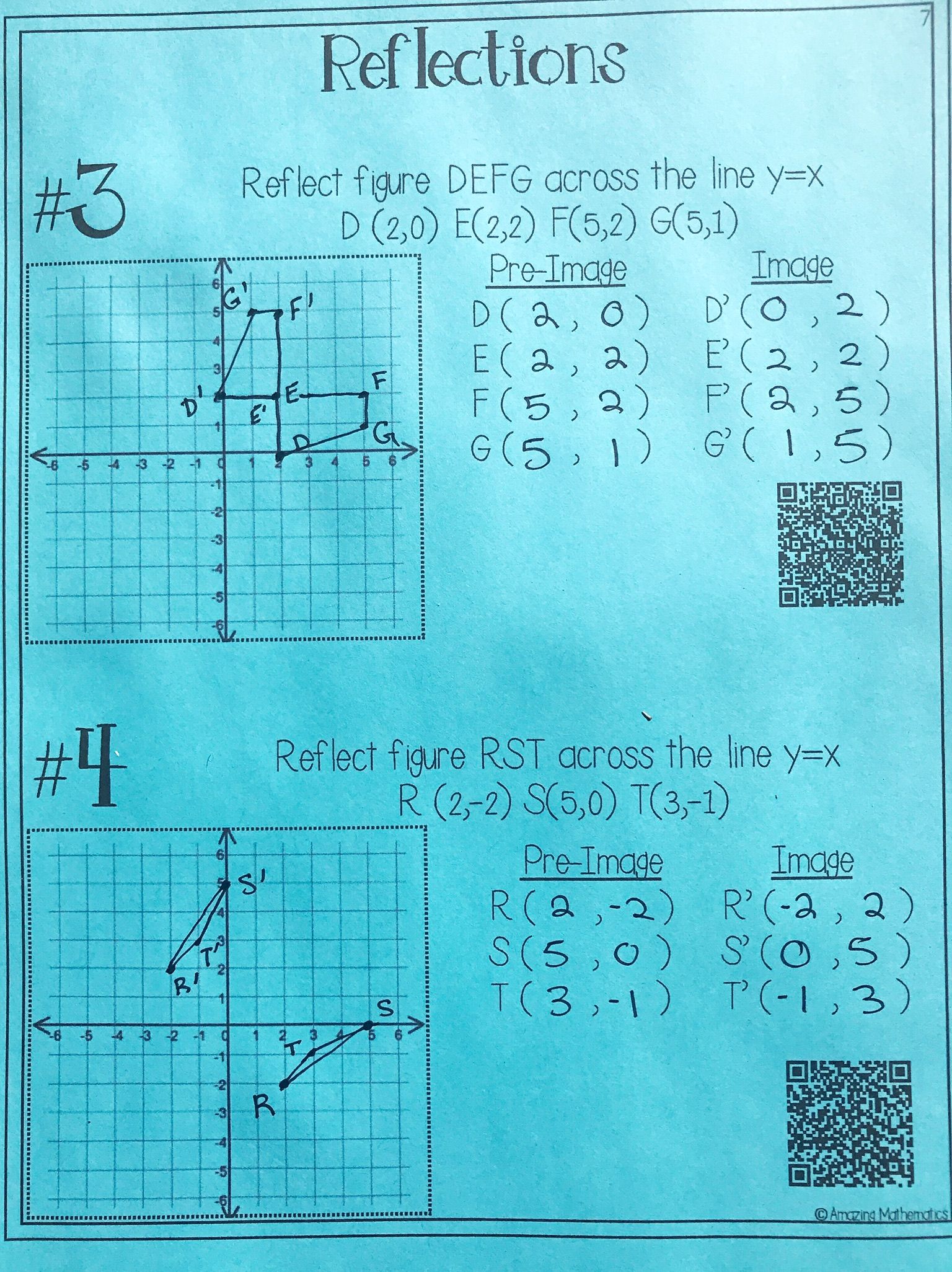
| Original Triangle | Translated Triangle |
|---|---|
| A (0, 0) | A’ (3, 2) |
| B (2, 0) | B’ (5, 2) |
| C (1, 2) | C’ (4, 4) |
- Example 2: Translate a rectangle 2 units down and 1 unit left.
| Original Rectangle | Translated Rectangle |
|---|---|
| A (0, 0) | A’ (-1, -2) |
| B (3, 0) | B’ (2, -2) |
| C (3, 2) | C’ (2, 0) |
| D (0, 2) | D’ (-1, 0) |
Key Concepts and Formulas
Here are some key concepts and formulas to keep in mind when working with translations:
- Translation Vector: The translation vector is represented by an arrow and defines the direction and distance of the translation.
- Distance Formula: The distance formula is used to calculate the distance between two points: d = √((x2 - x1)^2 + (y2 - y1)^2)
- Midpoint Formula: The midpoint formula is used to calculate the midpoint of a line segment: M = ((x1 + x2)/2, (y1 + y2)/2)
Tips and Tricks
Here are some tips and tricks to help you understand translations better:
- Visualize the Translation: Use graphs or diagrams to visualize the translation and make it easier to understand.
- Use Coordinates: Use coordinates to represent the original and translated shapes, making it easier to calculate distances and midpoints.
- Practice, Practice, Practice: Practice translating shapes and objects to become more comfortable with the concept.
💡 Note: Translations are an essential concept in geometry, and understanding them can help you solve more complex problems in the subject.
Common Mistakes and Misconceptions
Here are some common mistakes and misconceptions to watch out for when working with translations:
- Forgetting to Move the Shape: Make sure to move the shape along the translation vector and not just draw a new shape at the new position.
- Confusing Translation with Rotation: Translation and rotation are two different transformations, so make sure to understand the difference between them.
Real-World Applications of Translations
Translations have many real-world applications, including:
- Architecture: Translations are used in architecture to design buildings and structures.
- Computer Graphics: Translations are used in computer graphics to create animations and 3D models.
- Physics: Translations are used in physics to describe the motion of objects.
Conclusion
Translations are a fundamental concept in geometry, and understanding them can help you solve more complex problems in the subject. By visualizing the translation, using coordinates, and practicing, you can become more comfortable with the concept. Remember to watch out for common mistakes and misconceptions, and apply translations to real-world problems.
What is the difference between a translation and a rotation?
+
A translation moves a shape or object from one position to another without changing its size, shape, or orientation. A rotation turns a shape or object around a fixed point, changing its orientation but not its size or shape.
How do I calculate the distance of a translation?
+
The distance of a translation can be calculated using the distance formula: d = √((x2 - x1)^2 + (y2 - y1)^2)
What are some real-world applications of translations?
+
Translations have many real-world applications, including architecture, computer graphics, and physics.
Related Terms:
- Translation worksheets with answers
- Geometry Translations Worksheet Answer Key
- Translation practice worksheet pdf
- Translation Practice Worksheet answers pdf
- Rotations Geometry Worksheet
- Reflection Geometry Worksheet