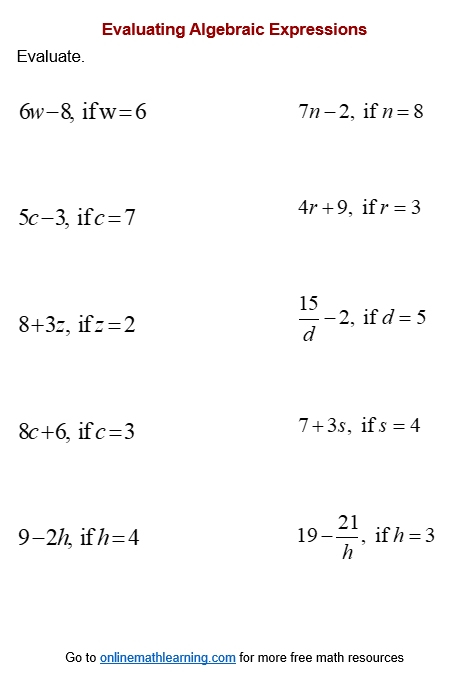Converting Repeating Decimals to Fractions Made Easy
Understanding Repeating Decimals
Repeating decimals are a fascinating aspect of mathematics, and they often pose a challenge for students. A repeating decimal is a decimal number that goes on indefinitely in a repeating pattern. For instance, 0.333… and 0.142857… are examples of repeating decimals. In this blog post, we will delve into the world of repeating decimals and explore the techniques for converting them into fractions.
Why Convert Repeating Decimals to Fractions?
There are several reasons why we might want to convert a repeating decimal to a fraction. One of the primary reasons is to make calculations easier. When we have a fraction, we can perform arithmetic operations like addition, subtraction, multiplication, and division with greater ease. Additionally, fractions are often more intuitive to understand, making it simpler to compare and analyze numbers.
Techniques for Converting Repeating Decimals to Fractions
There are several techniques for converting repeating decimals to fractions. In this section, we will explore two popular methods: the algebraic method and the calculator method.
Algebraic Method
The algebraic method is a straightforward technique for converting repeating decimals to fractions. Here’s a step-by-step guide to using this method:
- Identify the repeating pattern: Look for the repeating pattern in the decimal. For example, in the decimal 0.333…, the repeating pattern is 3.
- Set up an equation: Set up an equation based on the repeating pattern. For instance, if the repeating pattern is 3, we can set up the equation: 10x = 3.333…
- Subtract the non-repeating part: Subtract the non-repeating part of the decimal from the equation. In this case, we subtract 0.3 from both sides of the equation.
- Solve for x: Solve for x to find the fraction equivalent of the repeating decimal.
Let’s use this method to convert 0.333… to a fraction:
💡 Note: This method assumes that the repeating pattern starts immediately after the decimal point.
10x = 3.333…
Subtracting 0.3 from both sides gives:
9x = 3
Dividing both sides by 9:
x = 3⁄9
x = 1⁄3
Therefore, 0.333… is equivalent to the fraction 1⁄3.
Calculator Method
The calculator method is a more straightforward technique for converting repeating decimals to fractions. Here’s how to use a calculator to convert a repeating decimal to a fraction:
- Enter the repeating decimal: Enter the repeating decimal into your calculator.
- Find the fraction equivalent: Use the calculator’s built-in function to find the fraction equivalent of the repeating decimal.
For example, to convert 0.142857… to a fraction using a calculator, follow these steps:
Enter 0.142857 into your calculator.
Find the fraction equivalent using the calculator’s built-in function.
The calculator will display the fraction equivalent: 1⁄7.
Therefore, 0.142857… is equivalent to the fraction 1⁄7.
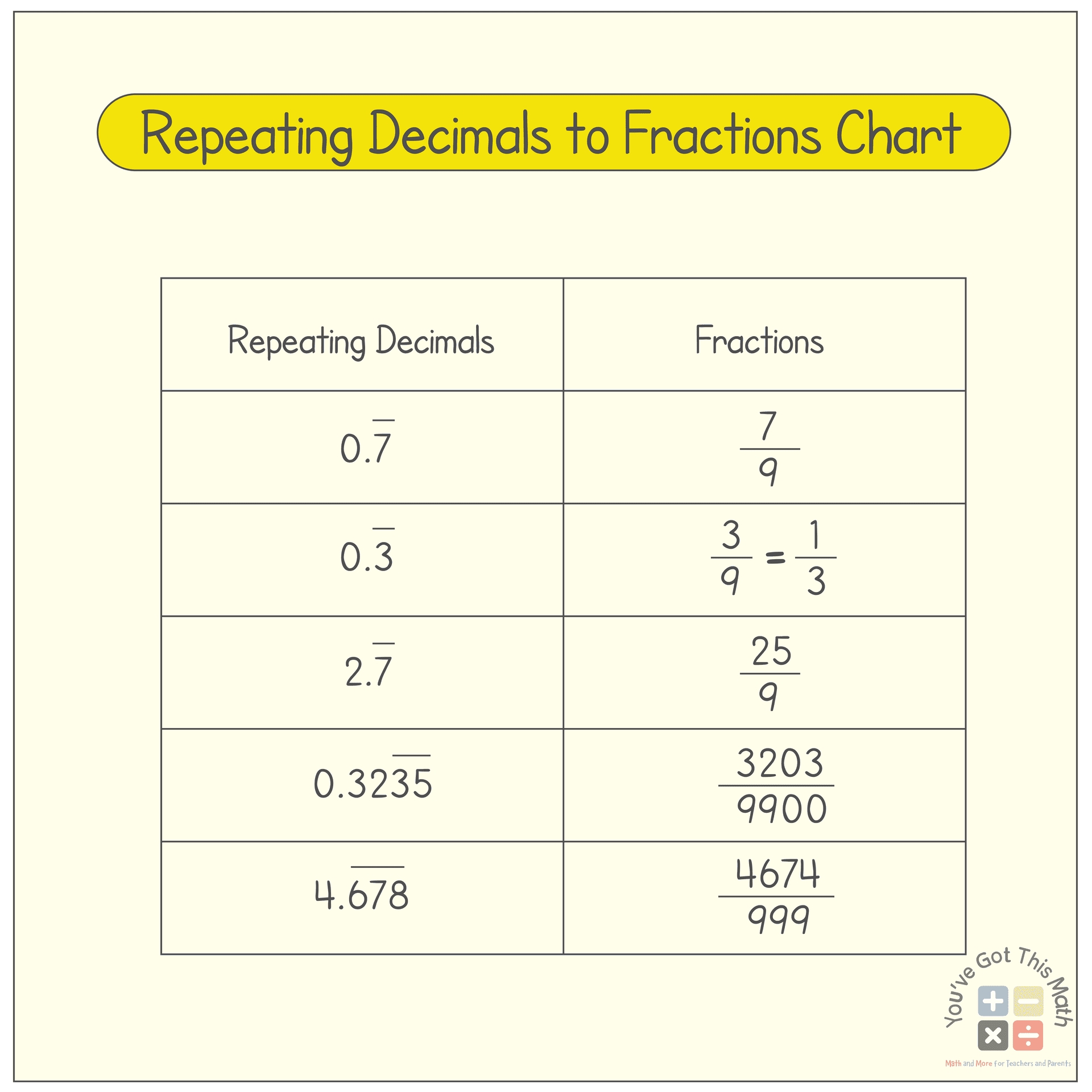
Common Repeating Decimals and Their Fraction Equivalents
Here are some common repeating decimals and their fraction equivalents:

| Repeating Decimal | Fraction Equivalent |
|---|---|
| 0.333... | 1/3 |
| 0.142857... | 1/7 |
| 0.6 | 2/3 |
| 0.428571... | 3/7 |
Conclusion
Converting repeating decimals to fractions is a useful skill that can make calculations easier and more intuitive. By using the algebraic method or the calculator method, you can easily convert repeating decimals to fractions. Remember to identify the repeating pattern, set up an equation, and solve for x to find the fraction equivalent of a repeating decimal.
In Summary
- Repeating decimals are decimal numbers that go on indefinitely in a repeating pattern.
- Converting repeating decimals to fractions makes calculations easier and more intuitive.
- The algebraic method and calculator method are two popular techniques for converting repeating decimals to fractions.
- Common repeating decimals include 0.333…, 0.142857…, and 0.6, which are equivalent to the fractions 1⁄3, 1⁄7, and 2⁄3, respectively.
What is a repeating decimal?
+A repeating decimal is a decimal number that goes on indefinitely in a repeating pattern.
Why convert repeating decimals to fractions?
+Converting repeating decimals to fractions makes calculations easier and more intuitive.
What are some common repeating decimals and their fraction equivalents?
+Some common repeating decimals and their fraction equivalents include 0.333… (1⁄3), 0.142857… (1⁄7), and 0.6 (2⁄3).
Related Terms:
- Converting decimals to fractions Worksheet