7 Ways to Master Translating Algebraic Expressions
Mastering the art of translating algebraic expressions is a crucial skill for any math enthusiast, student, or professional. Algebraic expressions are the building blocks of mathematical equations, and being able to translate them accurately is essential for solving problems and understanding complex mathematical concepts. In this article, we will explore seven ways to help you master the translation of algebraic expressions.
Understanding the Basics
Before diving into the techniques, it’s essential to understand the basics of algebraic expressions. An algebraic expression is a mathematical phrase that combines numbers, variables, and mathematical operations. Variables are letters or symbols that represent unknown values, while constants are numerical values.
1. Learn to Read Algebraic Expressions
To translate algebraic expressions, you need to learn to read them correctly. Start by understanding the order of operations, which is a set of rules that dictate the order in which mathematical operations should be performed. The order of operations is:
- Parentheses: Evaluate expressions inside parentheses first.
- Exponents: Evaluate any exponential expressions next.
- Multiplication and Division: Evaluate multiplication and division operations from left to right.
- Addition and Subtraction: Finally, evaluate any addition and subtraction operations from left to right.
📝 Note: This is often remembered using the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction).
2. Identify the Variables and Constants
Identifying the variables and constants in an algebraic expression is crucial for translation. Variables are typically represented by letters, while constants are numerical values. Be sure to distinguish between the two to avoid errors.
3. Simplify the Expression
Simplifying the expression can make it easier to translate. Combine like terms, and eliminate any unnecessary parentheses or brackets.
4. Use the Distributive Property
The distributive property is a powerful tool for translating algebraic expressions. It states that a single term can be distributed over multiple terms inside parentheses. For example:
2(x + 3) = 2x + 6
5. Combine Like Terms
Combining like terms is an essential step in translating algebraic expressions. Like terms are terms that have the same variable raised to the same power. For example:
2x + 3x = 5x
6. Use Algebraic Notation
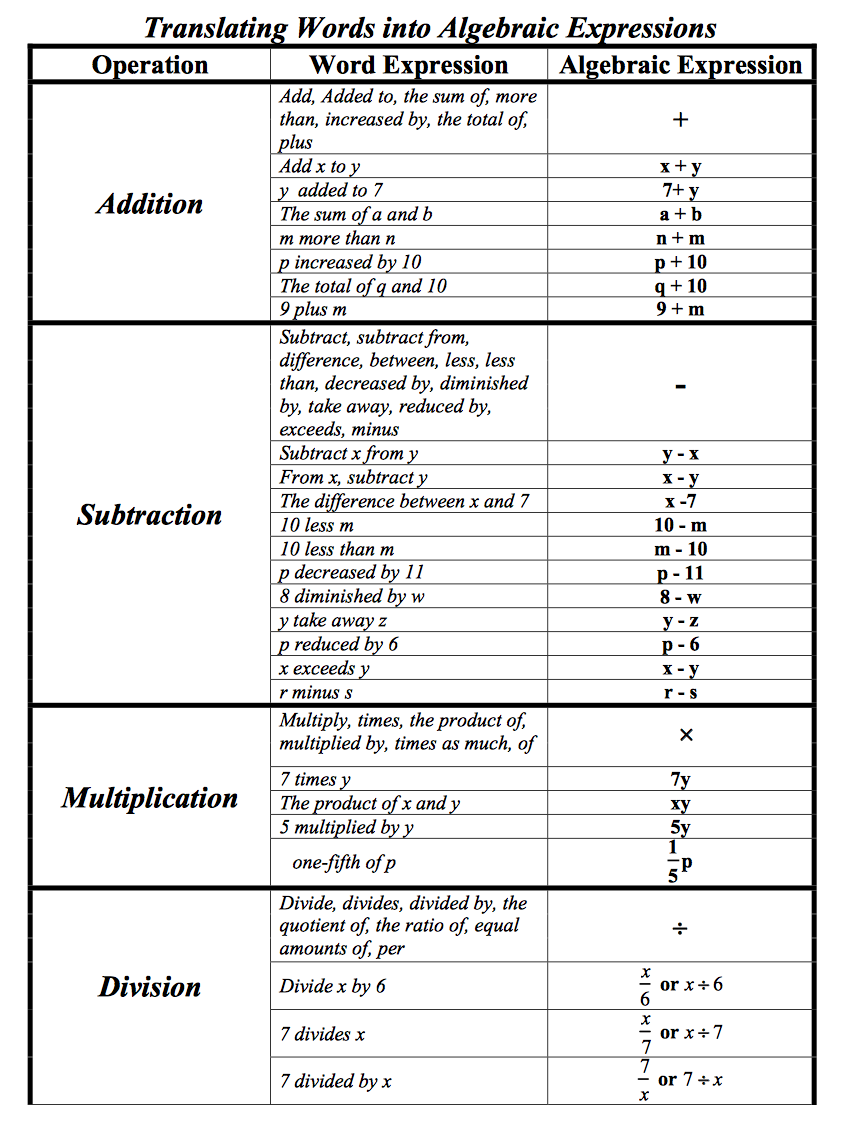
Algebraic notation is a shorthand way of writing algebraic expressions. It uses symbols and abbreviations to represent mathematical operations. Familiarize yourself with common algebraic notation symbols, such as:
- + for addition
- - for subtraction
- × or · for multiplication
- ÷ or / for division
7. Practice, Practice, Practice
Practice is key to mastering the translation of algebraic expressions. Start with simple expressions and gradually move on to more complex ones. Use online resources or worksheets to practice translating algebraic expressions.

| Expression | Translation |
|---|---|
| 2x + 5 | Two times x plus five |
| x - 3 | x minus three |
| 4(2x - 1) | Four times the quantity two x minus one |
By following these seven ways, you’ll be well on your way to mastering the translation of algebraic expressions. Remember to practice regularly and start with simple expressions before moving on to more complex ones.
In summary, mastering the translation of algebraic expressions requires a solid understanding of the basics, including the order of operations, variables, and constants. By simplifying expressions, using the distributive property, combining like terms, and practicing regularly, you’ll become proficient in translating algebraic expressions in no time.
What is an algebraic expression?
+An algebraic expression is a mathematical phrase that combines numbers, variables, and mathematical operations.
What is the order of operations?
+The order of operations is a set of rules that dictate the order in which mathematical operations should be performed. It is often remembered using the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction).
What is the distributive property?
+The distributive property is a rule that states that a single term can be distributed over multiple terms inside parentheses.
Related Terms:
- Translate algebraic expressions Worksheet pdf
- Translating Algebraic Expressions PDF
- Translating Algebraic expressions activity