Mastering Quadratic Functions Transformation Worksheet

Understanding Quadratic Functions Transformation
Quadratic functions are a fundamental concept in algebra, and understanding their transformations is crucial for solving problems and graphing functions. In this post, we will delve into the world of quadratic functions transformation and explore how to manipulate these functions to graph them accurately.
What are Quadratic Functions?
A quadratic function is a polynomial function of degree two, which means the highest power of the variable (usually x) is two. The general form of a quadratic function is:
f(x) = ax^2 + bx + c
where a, b, and c are constants, and a cannot be zero.
Types of Quadratic Functions Transformations
There are several types of transformations that can be applied to quadratic functions, including:
- Vertical Shift: Moving the graph up or down by adding or subtracting a constant to the function.
- Horizontal Shift: Moving the graph left or right by adding or subtracting a constant to the x-value.
- Vertical Stretch/Compression: Stretching or compressing the graph vertically by multiplying the function by a constant.
- Horizontal Stretch/Compression: Stretching or compressing the graph horizontally by multiplying the x-value by a constant.
- Reflection: Reflecting the graph across the x-axis or y-axis.
How to Apply Transformations to Quadratic Functions
To apply transformations to quadratic functions, you need to follow these steps:
- Identify the type of transformation you want to apply.
- Determine the value of the constant or coefficient that will be used for the transformation.
- Apply the transformation to the function by adding, subtracting, multiplying, or dividing the constant or coefficient.
Example 1: Vertical Shift
Suppose we want to shift the graph of f(x) = x^2 + 2x + 1 up by 3 units. We can do this by adding 3 to the function:
f(x) = x^2 + 2x + 1 + 3 f(x) = x^2 + 2x + 4
Example 2: Horizontal Shift
Suppose we want to shift the graph of f(x) = x^2 + 2x + 1 left by 2 units. We can do this by subtracting 2 from the x-value:
f(x) = (x + 2)^2 + 2(x + 2) + 1 f(x) = x^2 + 4x + 4 + 2x + 4 + 1 f(x) = x^2 + 6x + 9
Example 3: Vertical Stretch
Suppose we want to stretch the graph of f(x) = x^2 + 2x + 1 vertically by a factor of 2. We can do this by multiplying the function by 2:
f(x) = 2(x^2 + 2x + 1) f(x) = 2x^2 + 4x + 2
Example 4: Horizontal Stretch
Suppose we want to stretch the graph of f(x) = x^2 + 2x + 1 horizontally by a factor of 2. We can do this by multiplying the x-value by 2:
f(x) = (x/2)^2 + 2(x/2) + 1 f(x) = x^2⁄4 + x + 1
Example 5: Reflection
Suppose we want to reflect the graph of f(x) = x^2 + 2x + 1 across the x-axis. We can do this by multiplying the function by -1:
f(x) = - (x^2 + 2x + 1) f(x) = -x^2 - 2x - 1
🤔 Note: When reflecting a graph across the x-axis, the y-intercept changes sign.
Practice Worksheet
Now it’s your turn to practice applying transformations to quadratic functions! Complete the following worksheet:
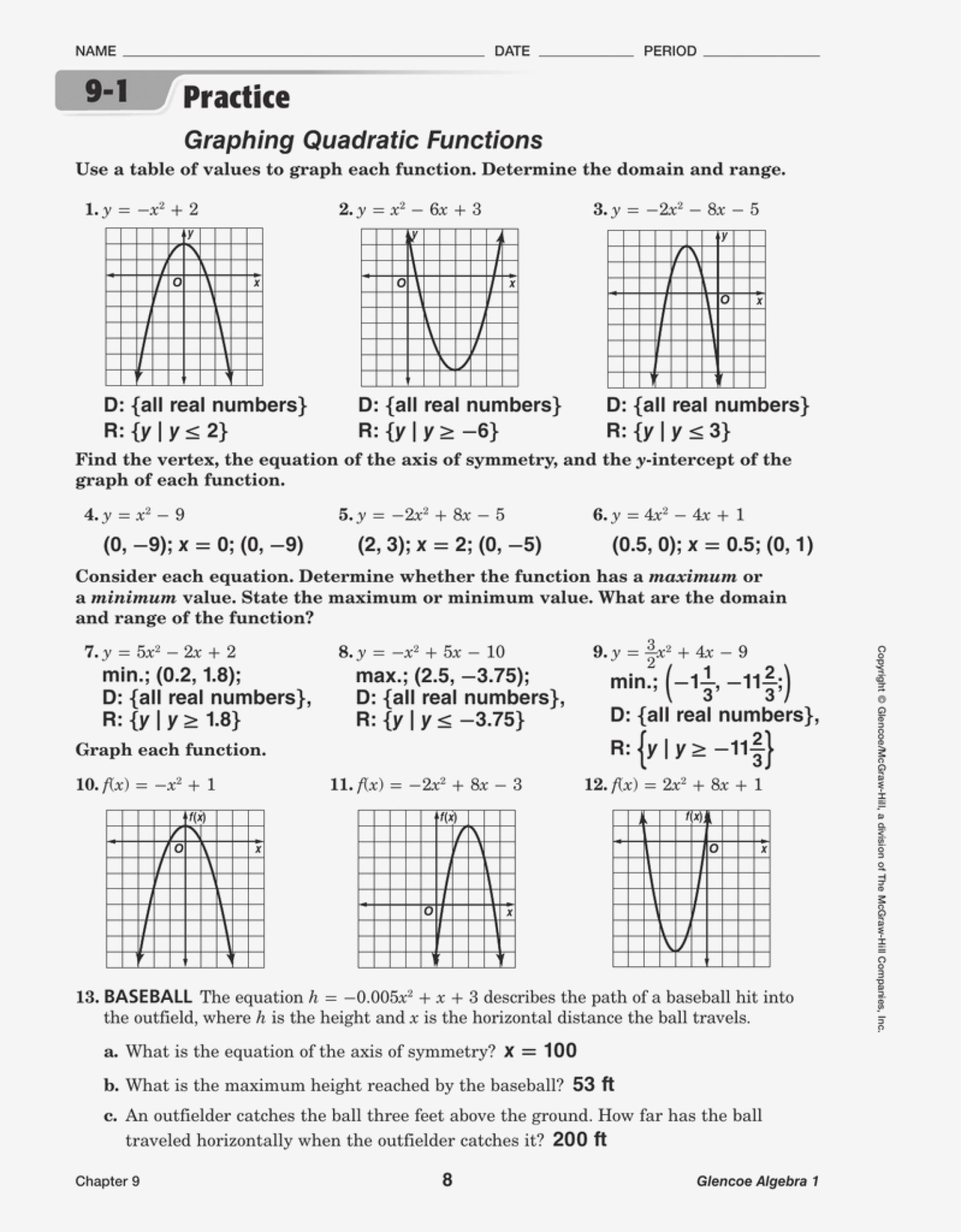
| Function | Transformation | New Function |
|---|---|---|
| f(x) = x^2 + 2x + 1 | Shift up by 2 units | |
| f(x) = x^2 + 2x + 1 | Shift left by 1 unit | |
| f(x) = x^2 + 2x + 1 | Stretch vertically by a factor of 3 | |
| f(x) = x^2 + 2x + 1 | Stretch horizontally by a factor of 2 | |
| f(x) = x^2 + 2x + 1 | Reflect across the y-axis |
Answers:
| Function | Transformation | New Function |
|---|---|---|
| f(x) = x^2 + 2x + 1 | Shift up by 2 units | f(x) = x^2 + 2x + 3 |
| f(x) = x^2 + 2x + 1 | Shift left by 1 unit | f(x) = (x + 1)^2 + 2(x + 1) + 1 |
| f(x) = x^2 + 2x + 1 | Stretch vertically by a factor of 3 | f(x) = 3(x^2 + 2x + 1) |
| f(x) = x^2 + 2x + 1 | Stretch horizontally by a factor of 2 | f(x) = (x/2)^2 + 2(x/2) + 1 |
| f(x) = x^2 + 2x + 1 | Reflect across the y-axis | f(x) = - (x^2 + 2x + 1) |
Conclusion
In conclusion, mastering quadratic functions transformation is an essential skill for any algebra student. By understanding how to apply different types of transformations, you can graph and solve quadratic functions with ease. Remember to practice, practice, practice, and you’ll become a pro at quadratic functions transformation in no time!
What is a quadratic function?
+A quadratic function is a polynomial function of degree two, which means the highest power of the variable (usually x) is two.
What are the different types of transformations that can be applied to quadratic functions?
+The different types of transformations that can be applied to quadratic functions include vertical shift, horizontal shift, vertical stretch/compression, horizontal stretch/compression, and reflection.
How do I apply a vertical shift to a quadratic function?
+To apply a vertical shift to a quadratic function, you add or subtract a constant to the function. For example, to shift the graph of f(x) = x^2 + 2x + 1 up by 2 units, you add 2 to the function: f(x) = x^2 + 2x + 1 + 2.
Related Terms:
- Graphing Quadratic Functions Worksheet pdf
- Vertex form Transformations Worksheet